Consider a uniform gas with density 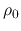 and pressure
and pressure 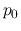 without motion
without motion 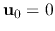 .
In this uniform gas distribution, we assume small perturbations.
As a result, the distributions of the density, the pressure and the velocity are perturbed from the uniform ones as
.
In this uniform gas distribution, we assume small perturbations.
As a result, the distributions of the density, the pressure and the velocity are perturbed from the uniform ones as
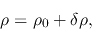 |
(2.27) |
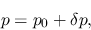 |
(2.28) |
and
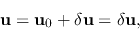 |
(2.29) |
where the amplitudes of perturbations are assumed much small, that is,
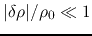 ,
,
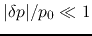 and
and
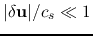 .
We assume the variables changes only in the
.
We assume the variables changes only in the 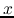 -direction.
In this case the basic equations for isothermal gas are
-direction.
In this case the basic equations for isothermal gas are
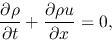 |
(2.30) |
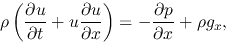 |
(2.31) |
and
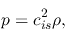 |
(2.32) |
where 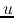 and
and 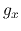 represent the
represent the 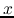 -component of the velocity and that of the gravity, respectively.
-component of the velocity and that of the gravity, respectively.
Using equations (2.27), (2.28), and (2.29),
equation (2.30) becomes
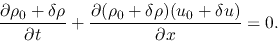 |
(2.33) |
Noticing that the amplitudes of variables with and without 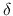 are completely different,
two equations are obtained from equation(2.33) as
are completely different,
two equations are obtained from equation(2.33) as
where the above is the equation for unperturbed state and the lower describes the relation between the
quantities with  .
Equation (2.34) is automatically satisfied by the assumption of uniform distribution.
In equation (2.35) the last term is equal to zero.
Equation of motion
.
Equation (2.34) is automatically satisfied by the assumption of uniform distribution.
In equation (2.35) the last term is equal to zero.
Equation of motion
 |
(2.36) |
gives the relationship between the terms containing only one variable with 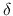 as follows:
as follows:
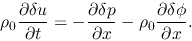 |
(2.37) |
The perturbations of pressure and density are related with each other as follows:
for the isothermal gas
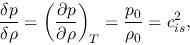 |
(2.38) |
and for isentropic gas
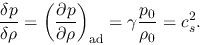 |
(2.39) |
Kohji Tomisaka
2012-10-03
![]() and pressure
and pressure ![]() without motion
without motion ![]() .
In this uniform gas distribution, we assume small perturbations.
As a result, the distributions of the density, the pressure and the velocity are perturbed from the uniform ones as
.
In this uniform gas distribution, we assume small perturbations.
As a result, the distributions of the density, the pressure and the velocity are perturbed from the uniform ones as