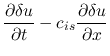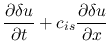If the self-gravity is ignorable, equation (2.35)
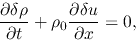 |
(2.40) |
and equation (2.37)
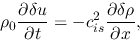 |
(2.41) |
where we assumed the gas is isothermal,
these two equations describe the propagation and growth of perturbations.
If the gas acts adiabatically, replace 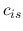 with
with 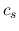 .
.
Making
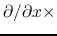 (2.40) and
(2.40) and
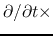 (2.41)
vanishes
(2.41)
vanishes 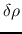 and we obtain
and we obtain
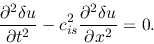 |
(2.42) |
Since this leads to
equation (2.42) has a solution that a wave propagates with a phase velocity of 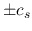 .
Since the displacement (
.
Since the displacement (
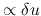 ) is parallel to the propagation direction
) is parallel to the propagation direction 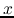 ,
and the restoring force comes from the pressure, this seems the sound wave.
,
and the restoring force comes from the pressure, this seems the sound wave.
Subsections
Kohji Tomisaka
2012-10-03
![]() (2.40) and
(2.40) and
![]() (2.41)
vanishes
(2.41)
vanishes ![]() and we obtain
and we obtain