Consider 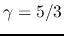 gas, the gravitational energy is equal to
twice of the kinetic+thermal energy [eq.(2.120)]
in the equilibrium state.
This gives a definition of Virial mass.
The kinetic energy is obtained from the 3D velocity dispersion
gas, the gravitational energy is equal to
twice of the kinetic+thermal energy [eq.(2.120)]
in the equilibrium state.
This gives a definition of Virial mass.
The kinetic energy is obtained from the 3D velocity dispersion
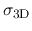 as
as
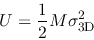 |
(2.121) |
for globular clusters and elliptical galaxies,
where 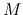 is the mass of the object.
For molecular cloud this is estimated from the width of the emission line.
Equation (E.7) of
Appendix E gives
is the mass of the object.
For molecular cloud this is estimated from the width of the emission line.
Equation (E.7) of
Appendix E gives
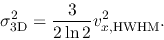 |
(2.122) |
where
 is the half width of the half maximum of
the emission line (if the radiation is optically thin;
see Fig.E.1).
Since the gravitational energy is proportional to
is the half width of the half maximum of
the emission line (if the radiation is optically thin;
see Fig.E.1).
Since the gravitational energy is proportional to 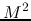 as
as
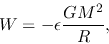 |
(2.123) |
the Virial theorem gives
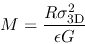 |
(2.124) |
if the surface term is ignored.
This gives an estimation of mass of astronomical object.
Kohji Tomisaka
2012-10-03
![]() gas, the gravitational energy is equal to
twice of the kinetic+thermal energy [eq.(2.120)]
in the equilibrium state.
This gives a definition of Virial mass.
The kinetic energy is obtained from the 3D velocity dispersion
gas, the gravitational energy is equal to
twice of the kinetic+thermal energy [eq.(2.120)]
in the equilibrium state.
This gives a definition of Virial mass.
The kinetic energy is obtained from the 3D velocity dispersion
![]() as
as