Figure 3.7:
Tightly wound (left) vs loosely wound (right) spirals.
 |
We assume the wave driven by the self-gravity has a form of tightly-wound spiral
[Fig.3.7(left)].
When we move radially, the density 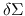 varies rapidly.
While, it changes its amplitude slowly in the azimuthal direction.
In a mathematical expression, if we write the density perturbation
varies rapidly.
While, it changes its amplitude slowly in the azimuthal direction.
In a mathematical expression, if we write the density perturbation 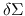 as
as
![\begin{displaymath}
\delta \Sigma =A(R,t)\exp[i m\phi+i f(R,t)],
\end{displaymath}](img861.png) |
(3.22) |
where the amplitude of spiral 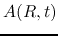 is a slowly varing function of
is a slowly varing function of 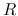 ,
a tightly wound spiral means the shape function varies fast (the radial wavenumber
,
a tightly wound spiral means the shape function varies fast (the radial wavenumber
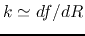 is large enough).
We consider the gravitational force from the vicinity of
is large enough).
We consider the gravitational force from the vicinity of 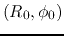 , since the
, since the 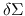 oscillates
and cancels even if we integrate over large region.
Thus,
oscillates
and cancels even if we integrate over large region.
Thus,
![\begin{displaymath}
\delta \Sigma (R,\phi,t)\simeq \Sigma_a \exp [ik(R_0,t)(R-R_0)],
\end{displaymath}](img865.png) |
(3.23) |
where
![\begin{displaymath}
\Sigma_a=A(R_0,t)\exp[im\phi_0+f(R_0,t)].
\end{displaymath}](img866.png) |
(3.24) |
Notice that the density perturbation [eq.(3.23)] is similar to that studied in
 2.6.
The potential should be expressed in a similar form to equation (2.64) as
2.6.
The potential should be expressed in a similar form to equation (2.64) as
![\begin{displaymath}
\delta \Phi \simeq -\frac{2\pi G \Sigma_a}{\vert k\vert}\exp[ik(R_0,t)(R-R_0)],
\end{displaymath}](img867.png) |
(3.25) |
which simply means
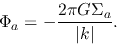 |
(3.26) |
If we set 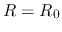 , we obtain our final result for the potential due to the surface density perturbation
, we obtain our final result for the potential due to the surface density perturbation
![\begin{displaymath}
\delta \Phi (R, \phi, t) \simeq -\frac{2 \pi G}{\vert k\vert}A(R,t)\exp[im\phi+f(R,t)].
\end{displaymath}](img870.png) |
(3.27) |
Differentiating this equation with 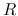 and ignoring the term
and ignoring the term 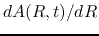 compared to that of
compared to that of
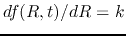 , we obtain
, we obtain
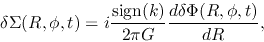 |
(3.28) |
Neglecting the terms 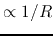 compared to the terms containing
compared to the terms containing
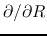 ,
equations (3.19), (3.20), and (3.21) are rewritten as
,
equations (3.19), (3.20), and (3.21) are rewritten as
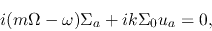 |
(3.29) |
![\begin{displaymath}
u_a [\kappa^2 -(m\Omega -\omega)^2] = (m\Omega - \omega) k (\Phi_a + h_a),
\end{displaymath}](img877.png) |
(3.30) |
and
![\begin{displaymath}
v_a [\kappa^2 -(m\Omega -\omega)^2] = i \frac{\kappa^2}{2\Omega} k (\Phi_a + h_a),
\end{displaymath}](img878.png) |
(3.31) |
Using these equations [(3.29), (3.30), and
(3.31)],
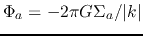 , and
, and
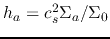 ,
we obtain the dispersion relation for the self-gravitating instability of the rotating gaseous thin disk
,
we obtain the dispersion relation for the self-gravitating instability of the rotating gaseous thin disk
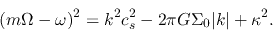 |
(3.32) |
Generally speaking, the epicyclic frequency depends on the rotation law but is in the range of
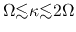 (see Table 3.1 for
(see Table 3.1 for 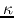 for typical rotation laws).
It is shown that the system is stabilized due to the epicyclic frequency compared with a nonrotating
thin disk [eq.(2.65)].
for typical rotation laws).
It is shown that the system is stabilized due to the epicyclic frequency compared with a nonrotating
thin disk [eq.(2.65)].
Table 3.1:
Epicyclic frequency vs rotation law.
| Rotation |
 |
Rigid-body rotation 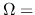 const. const. |
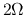 |
Flat rotation 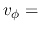 const. const. |
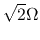 |
Kepler rotation
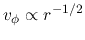 |
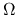 |
Kohji Tomisaka
2012-10-03
![]() varies rapidly.
While, it changes its amplitude slowly in the azimuthal direction.
In a mathematical expression, if we write the density perturbation
varies rapidly.
While, it changes its amplitude slowly in the azimuthal direction.
In a mathematical expression, if we write the density perturbation ![]() as
as
![]() compared to the terms containing
compared to the terms containing
![]() ,
equations (3.19), (3.20), and (3.21) are rewritten as
,
equations (3.19), (3.20), and (3.21) are rewritten as