If the atoms and molecules are permeated by magnetic field 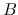 ,
in the normal Zeeman splitting,
the transition splits into three lines
,
in the normal Zeeman splitting,
the transition splits into three lines
where
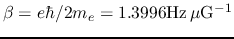 is
the Bohr magneton constant.
This comes from the fact that the upper and lower levels
are splited into
is
the Bohr magneton constant.
This comes from the fact that the upper and lower levels
are splited into
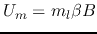 using the magnetic quantum number
using the magnetic quantum number 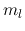 .
HI
.
HI 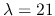 cm, OH (maser emissions and thermally excited emissions),
H
cm, OH (maser emissions and thermally excited emissions),
H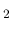 O maser emissions are used to measure the magnetic field strength.
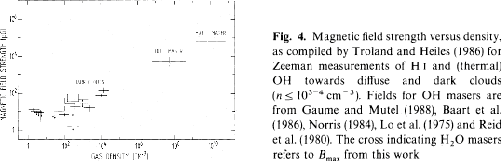
Figure 4.4 represents the correlation
between the magnetic field strength and gas density compiled
by Fiebig & Guesten (1989),
which indicates that
O maser emissions are used to measure the magnetic field strength.
Figure 4.4 represents the correlation
between the magnetic field strength and gas density compiled
by Fiebig & Guesten (1989),
which indicates that 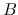 is approximately proportional to
is approximately proportional to 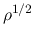
Figure 4.4:
 |
Kohji Tomisaka
2012-10-03
![]() ,
in the normal Zeeman splitting,
the transition splits into three lines
,
in the normal Zeeman splitting,
the transition splits into three lines