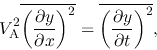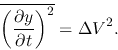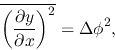Chandrasekhar & Fermi (1953) obtained the strength of interstellar
magnetic field.
Applying the same method to the molecular cloud,
Crutcher et al. (2004) obtained the magnetic field strength in the plane of the sky
in three prestellar clouds as
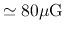 (L183),
(L183),
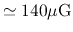 (L1544),
and
(L1544),
and
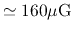 (L43).
The method is as follows:
Using the phase velocity of transverse Alfvén wave,
(L43).
The method is as follows:
Using the phase velocity of transverse Alfvén wave,
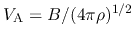 ,
the wave is described as
,
the wave is described as
![\begin{displaymath}
y=A\cos\left[k(x-V_{\rm A}t)\right],
\end{displaymath}](img1118.png) |
(4.38) |
where 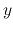 is a displacement in the plane of the sky and perpendicular
to the mean magnetic field.
This gives
is a displacement in the plane of the sky and perpendicular
to the mean magnetic field.
This gives
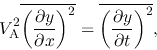 |
(4.39) |
where 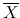 represents the time average.
The rhs of the equation, which is the one-dimensional velocity dispersion
in
represents the time average.
The rhs of the equation, which is the one-dimensional velocity dispersion
in 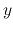 direction, seems to be equal to
the velocity dispersion in the line-of-sight
direction, seems to be equal to
the velocity dispersion in the line-of-sight 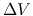 as
as
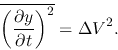 |
(4.40) |
The lhs of the equation is given with a dispersion
of polarization direction 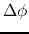 (rad)
(rad)
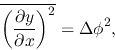 |
(4.41) |
in which the lhs is measured by the wave-pattern of the Alfvén wave.
Therefore, the magnetic field strength is given as
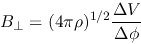 |
(4.42) |
Kohji Tomisaka
2012-10-03