Next: Ambipolar Diffusion Up: Subcritical Cloud vs Supercritical Previous: Chandrasekhar-Fermi Method Contents
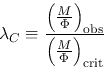 |
(4.43) |
| (4.44) |
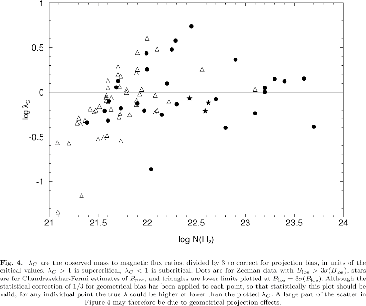 |
Figure 4.5 indicates
cloud cores are more or less found near the critical mass-to-flux ratio.
They are not distributed either
in the regions
![]() (very supercritical)
or
(very supercritical)
or
![]() (very subcritical).
(very subcritical).