Below
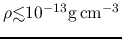 , gas is essentially isothermal
, gas is essentially isothermal
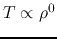 .
This corresponds to points number 1-3 of Figure 4.16.
Since internal energy of gas is transferred to the thermal energy of dusts by collisions,
the main coolant in this regime is the dust thermal radiation.
The cooling rate per mass is
.
This corresponds to points number 1-3 of Figure 4.16.
Since internal energy of gas is transferred to the thermal energy of dusts by collisions,
the main coolant in this regime is the dust thermal radiation.
The cooling rate per mass is
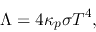 |
(4.107) |
where
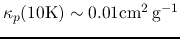 and
and 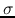 represent Planck mean absorption coefficient and the Stephan-Boltzman constant.
Main heating process for
represent Planck mean absorption coefficient and the Stephan-Boltzman constant.
Main heating process for
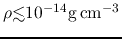 is
cosmic-ray heating:
is
cosmic-ray heating:
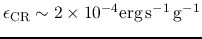 (Goldsmith & Langer 1978).
Balance between these two majors asks that temperature is constant as
(Goldsmith & Langer 1978).
Balance between these two majors asks that temperature is constant as
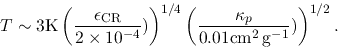 |
(4.108) |
Heating rate due to dynamical compression,
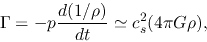 |
(4.109) |
increases according to the contraction
and it balances with the above cooling at the density
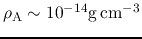 (Masunaga, Miyama, & Inutsuka 1998).
(Masunaga, Miyama, & Inutsuka 1998).
The cloud in this phase experiences the dynamical contraction as described in section 4.5.
Structure of 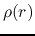 and
and 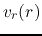 is well represented by the Larson-Penston self-similar
solution.
is well represented by the Larson-Penston self-similar
solution.
Kohji Tomisaka
2012-10-03
![]() and
and ![]() is well represented by the Larson-Penston self-similar
solution.
is well represented by the Larson-Penston self-similar
solution.