Abstract
Authors
Details
|
Cosmological solutions to the Lithium problem:
Big-bang nucleosynthesis with photon cooling,
X-particle decay and a primordial magnetic field
2014. 07. 01.
 |
|
 |
Abstract
|
|
The 7Li abundance calculated in BBN with the baryon-to-photon ratio fixed from fits to the CMB power spectrum is inconsistent with the observed lithium abundances on the surface of metal-poor halo stars. Previous cosmological solutions proposed to resolve this 7Li problem include photon cooling (possibly via the Bose-Einstein condensation of a scalar particle) or the decay of a long-lived X-particle (possibly the next-to-lightest supersymmetric particle). In this paper we reanalyze these solutions, both separately and in concert. We also introduce the possibility of a primordial magnetic field (PMF) into these models. We constrain the X-particles and the PMF parameters by the observed light element abundances using a likelihood analysis to show that the inclusion of all three possibilities leads to an optimum solution to the lithium problem. We deduce allowed ranges for the X-particle parameters and energy density in the PMF that can solve 7Li problem.
|
|
 |
|
 |
Authors
|
|
|
  |
 |
|
 |
Details
|
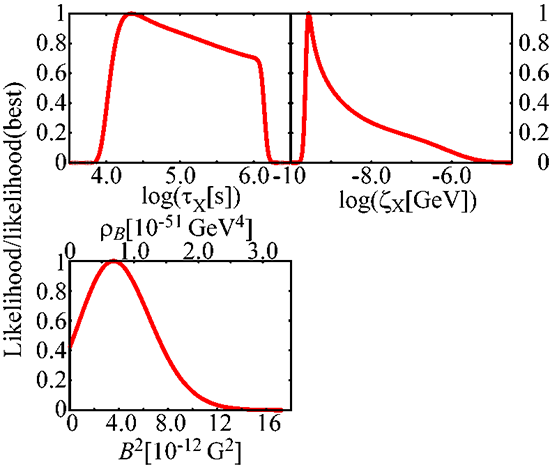
We have calculated BBN taking into account three possible cosmological extensions of the standard BBN. These include photon cooling, the radiative decay of X particles, and the possible existence of a PMF. In particular, we consider the possible combination of all three paradigms simultaneously in a new hybrid model. We then utilized a maximum likelihood analysis to deduce constraints on the parameters characterizing the X particles (τX[s], ζX[s]) and the energy density of the PMF (ρB = B2/8π) from the observed abundances of light elements up to Li.
|
|
FIG. 2;
Constraint on the X particle parameters and the PMF strength and energy density.
|
From FIG. 2, as a result, we obtained ranges for the X-particle parameters given by
4.06 < log (τX[s]) < 6.10 (95% C.L.),
-9.70 < log (ζX[GeV]) < -6.23 (95% C.L.),
e also find that the hybrid model with a PMF gives the better likelihood than that without a PMF,
and the best fit and 2 σ upper bound on the energy density of the PMF are
B = 1.89nG at a = 1.0 (the best fit),
B < 3.05nG at a = 1.0 (95% C.L.).
We discussed the degeneracy between the parameters of the X particle and the PMF.
Since the parameters of X particle are mainly constrained by the D and 7Li abundances, while the energy density of the PMF is constrained by the 4He abundance, we found there are no significant degeneracies between parameters of the PMF and the X particle.
|
|
  |
|
|
|

