Next: ソース項vs流束の発散 Up: gravity Previous: 重力流束テンソル
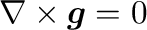 が重要
が重要
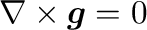 が条件と
なっていることに注意する必要がある。
これを理解するには、式(8)の一部分を書き下してみれば良い。
式(10)は
が条件と
なっていることに注意する必要がある。
これを理解するには、式(8)の一部分を書き下してみれば良い。
式(10)は
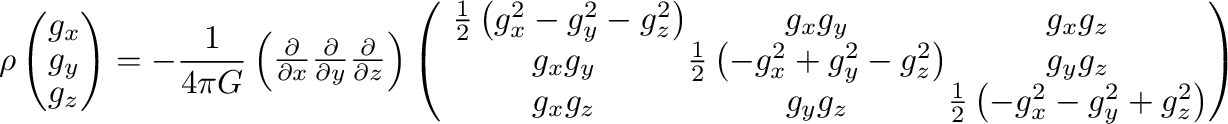 |
(11) |
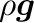 の
の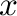 成分は
成分は
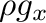 |
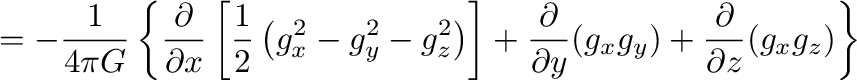 |
(12) |
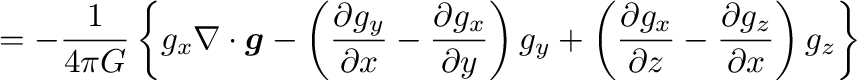 |
(13) |
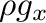 を与える。
を与える。
短く言うとMHG2021の式(34)
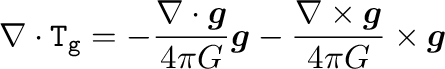 |
(14) |
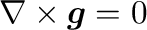 の条件を満たすときにのみ、
式(10)が成り立つことになる。
の条件を満たすときにのみ、
式(10)が成り立つことになる。
なお、MHDにおけるローレンツ力もマックスウェル応力の発散の形に書き直すと、
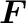 |
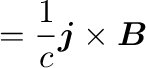 |
|
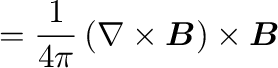 |
||
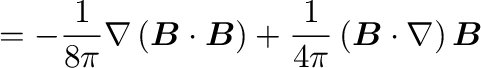 |
||
![$\displaystyle =-\nabla\cdot\left[\frac{1}{8\pi}(\bm{B}\cdot\bm{B})\mathtt{I}-\f...
...}\bm{B}\otimes\bm{B}\right]
-\frac{1}{4\pi}\bm{B}\left(\nabla\cdot\bm{B}\right)$](img31.png) |
(15) |
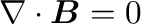 を満足する場合のみ、
(そして
を満足する場合のみ、
(そして
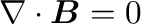 はマックスウェル方程式の一部であるが)
マックスウエル応力の磁場成分、
はマックスウェル方程式の一部であるが)
マックスウエル応力の磁場成分、
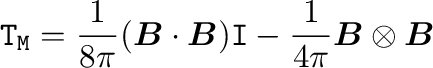 |
(16) |