式(1)と式(7)は数値計算上の取り扱いが異なる。
式(1)は、
![$\displaystyle \frac{\partial \rho\bm{v}}{\partial t}+\nabla\cdot[\rho\bm{v}\otimes\bm{v}+p\mathtt{I}]=0$](img33.png) |
(17) |
と
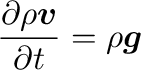 |
(18) |
に分解して解くことになるため、厳密な運動量保存は成り立たなくなる。
一方、式(7)を解く立場では、
のように時間推進するが、時間発展が流束の発散の形で書かれているから、
自己重力流体の問題に対して、外部境界での流束がなければ、厳密に運動量保存が成り立つ。
Athena(Stone+2008)およびver.19までのAthena++(Stone+2020)では、
式(7)の形式を採用しており、
直ぐ下で見る方法で評価した重力テンソルを運動量流束テンソルに加えて
移流する(つまり式(7)を解く)ことが行われていた。
しかし、密度分布に強い偏りが生じた場合などで、
重力場に回転(rot/curl)およびそれを起源とする誤差を生じる問題がMHG21で指摘された
(MHG21の図6)。
Stone+2008,2020の重力テンソル(式(8))の評価法は、
である。
ここで、整数の添え字はセル中心を、半整数の添え字はセル表面での値を表す。
MHG21は、ソース項に重力を残す式(1)の方法で、
重力テンソルの発散と同じ性質を持つ、
運動量に誤差を生じないスキームを提案した。
MHG21は、重力テンソルの評価を、Stone+2008,2020のものから、対角成分だけ変更し、
以下のような物にした。
(代表的対角成分である式(20)を式(23)に変更。)
こう取ると、MHG21の補遺Aで示されるように、このテンソルの発散(の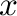 成分)は
となるが、右辺は
成分)は
となるが、右辺は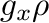 の自然な差分表現になっており、最初の項
の自然な差分表現になっており、最初の項
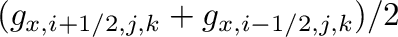 は、セル中心での
は、セル中心での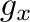 が
が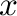 方向に面したセル表面での
加速度
方向に面したセル表面での
加速度
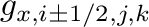 の算術平均で与えられること、
2項目は、セル表面の
の算術平均で与えられること、
2項目は、セル表面の
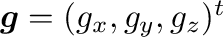 から計算される発散がセル中心の
から計算される発散がセル中心の
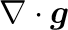 を
与えることを示している。
つまり、そのようにとれば、右辺のソース項は重力テンソルTの発散で表される
ことがわかる。
を
与えることを示している。
つまり、そのようにとれば、右辺のソース項は重力テンソルTの発散で表される
ことがわかる。
![$\displaystyle \frac{\partial \rho\bm{v}}{\partial t}+\nabla\cdot[\rho\bm{v}\otimes\bm{v}+p\mathtt{I}]=0$](img33.png)
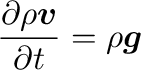
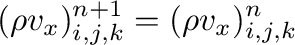
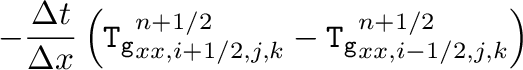
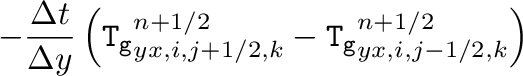
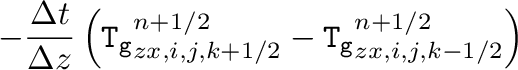
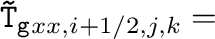
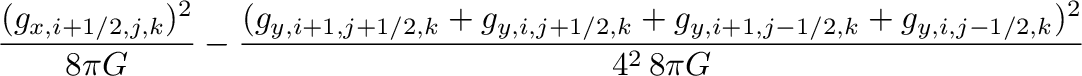
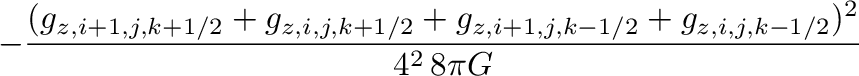
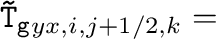
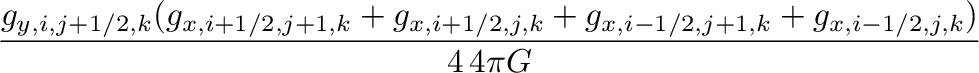
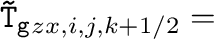
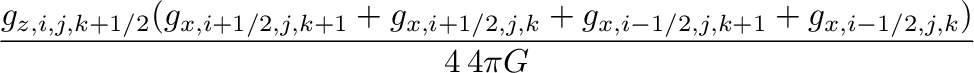
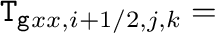
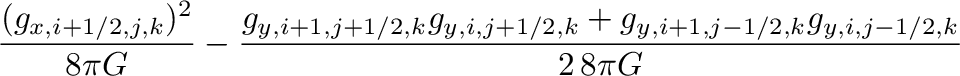
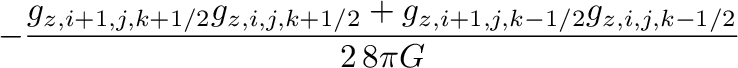

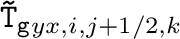
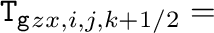
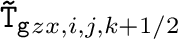
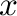 成分)は
となるが、右辺は
成分)は
となるが、右辺は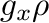 の自然な差分表現になっており、最初の項
の自然な差分表現になっており、最初の項
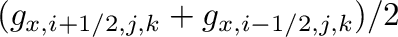 は、セル中心での
は、セル中心での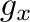 が
が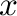 方向に面したセル表面での
加速度
方向に面したセル表面での
加速度
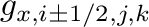 の算術平均で与えられること、
2項目は、セル表面の
の算術平均で与えられること、
2項目は、セル表面の
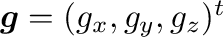 から計算される発散がセル中心の
から計算される発散がセル中心の
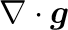 を
与えることを示している。
つまり、そのようにとれば、右辺のソース項は重力テンソルTの発散で表される
ことがわかる。
を
与えることを示している。
つまり、そのようにとれば、右辺のソース項は重力テンソルTの発散で表される
ことがわかる。