Next: まとめ Up: gravity Previous: ソース項で取るべき差分
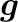 の回転は
となる。
一つの成分について調べてみれば十分なので、
の回転は
となる。
一つの成分について調べてみれば十分なので、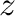 成分に着目し、
この式(36)の
成分に着目し、
この式(36)の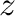 成分に
成分に
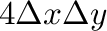 を掛けると
それぞれの項は、図1の
を掛けると
それぞれの項は、図1の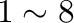 の長さ
の長さ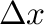 および
および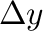 の
線分に対する線積分を与える。
例えば、第1項は
の
線分に対する線積分を与える。
例えば、第1項は
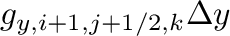 であるが、図1の太い矢印部分の
であるが、図1の太い矢印部分の
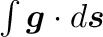 の積分値の評価となっている。
式(37)は
の積分値の評価となっている。
式(37)は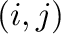 を取り囲む8個のセルを周回する積分
を取り囲む8個のセルを周回する積分
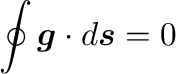 |
(38) |
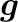 がポテンシャル場であれば(そして“ポテンシャル場的”に差分が作られていれば)消えることになる。
それは式(37)に、
がポテンシャル場であれば(そして“ポテンシャル場的”に差分が作られていれば)消えることになる。
それは式(37)に、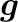 の具体的な形、
式(32)、(33)、(34)を入れてみれば、
の具体的な形、
式(32)、(33)、(34)を入れてみれば、
 |
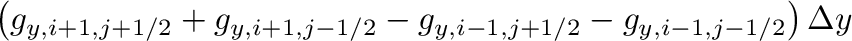 |
|
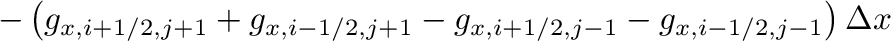 |
||
 |
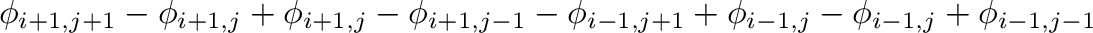 |
|
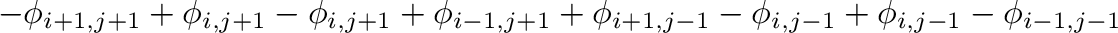 |
||
 |
0 | (39) |