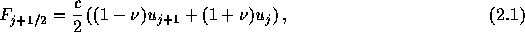
さて、前章で見たように、 空間1次精度風上差分は単調な解を与えるが、飛びが時間的に鈍ってくるという欠点 を持ち、空間2次精度のスキームは、飛びの鈍りは押えられるが、振動を生じるという 欠点を持っている。
そこで、なるべく空間2次精度を保ちながら、振動を生じる(短波長の振動の原因 となる)飛びの部分では空間1次精度に自動的に落ちるようなスキームはないかを 考える。
Lax-Wendroffスキーム(数値流速は
であらわされる)と空間1次精度スキーム(数値流速は

であらわされる)の中間のものを考える。 式(2.1)は
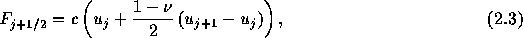
と書き直せるので、目標とする数値流速の形を
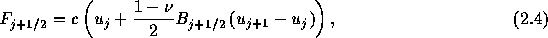
とし、空間1次精度に落すべきところでは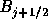 が0になるようなものを
考える。そこで
が0になるようなものを
考える。そこで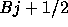 のことを流束制限関数と呼ぶ。
上の式を時間進化を表す式に代入すると、
のことを流束制限関数と呼ぶ。
上の式を時間進化を表す式に代入すると、
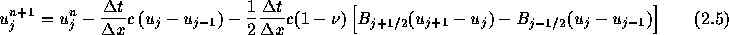
または、
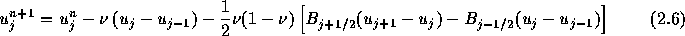
となる。
これから、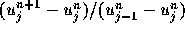 を計算すると、
を計算すると、
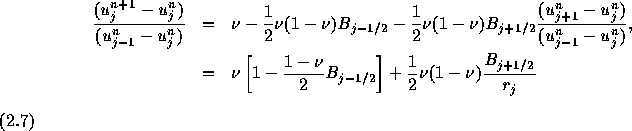
ここで

である。
この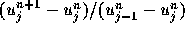 が0と1の間にあれば
単調であるべき部分でその単調性が保証され得る(monotonicity preverving)
(数値的振動をさけるための十分条件)。
つまり、
が0と1の間にあれば
単調であるべき部分でその単調性が保証され得る(monotonicity preverving)
(数値的振動をさけるための十分条件)。
つまり、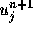 は
は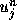 と
と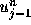 の間にあれば、
新たなピークを作ることもしないし、振動の振幅を大きくすることもないことに
よっている。
の間にあれば、
新たなピークを作ることもしないし、振動の振幅を大きくすることもないことに
よっている。
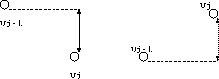
Figure 2.1: 流束制限の説明。
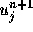 は
は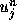 と
と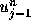 の間にあれば、
新たなピークを作ることもしないし、振動の振幅を大きくすることもない。
の間にあれば、
新たなピークを作ることもしないし、振動の振幅を大きくすることもない。
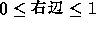 となる条件を考える。
となる条件を考える。
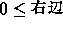 の方は
の方は
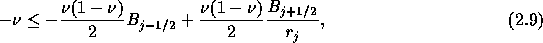
であるから、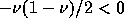 で割ると、
で割ると、
となる。
一方、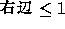 の方は
の方は
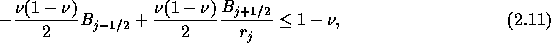
であるから、同じように
となる。式(2.10)、(2.12)より、数値的振動を避ける ために流束制限関数のもつべき条件は、
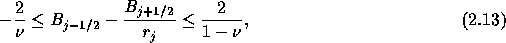
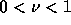 なので、
すくなくとも
なので、
すくなくとも
であれば流束制限関数のもつべき条件を満足できる。
ここでさらに流束制限関数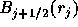 に具体的条件をあたえるために、
これを満足する十分条件を考える。
に具体的条件をあたえるために、
これを満足する十分条件を考える。
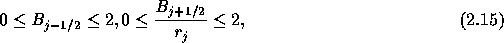
となっていれば、式(2.14)を満足することはすぐにわかる。
r<0の場合、すなわち、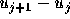 と
と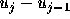 の符合が
異なっている場合、これは急激に振動が起こっているような場所に相当し、
後ろ側の条件から、
の符合が
異なっている場合、これは急激に振動が起こっているような場所に相当し、
後ろ側の条件から、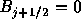 となっていなければならない。
それにともなって、数値流束は1次精度風上差分のものに落ちる。
r>0の場合、図2.2の
となっていなければならない。
それにともなって、数値流束は1次精度風上差分のものに落ちる。
r>0の場合、図2.2の
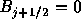 より上、
より上、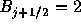 より下で、
より下で、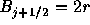 より右下がわにBが来れば良いことがわかる。
Lax-Wendroffの数値流束に一致するのが、B=1の場合であったから、
なるべく
より右下がわにBが来れば良いことがわかる。
Lax-Wendroffの数値流束に一致するのが、B=1の場合であったから、
なるべく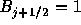 となるように選ぶ。
これを満足する流束制限関数のうち代表的なminmod関数とsuperbee関数を
図2.2に示した。
となるように選ぶ。
これを満足する流束制限関数のうち代表的なminmod関数とsuperbee関数を
図2.2に示した。
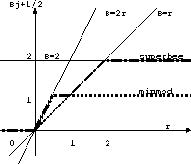
Figure 2.2: 代表的な流束制限関数。
minmod関数、superbee関数の例があげてある。
これまでの説明で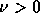 としてきた(風上をjの小さい方にとってきた)。
この時は、
としてきた(風上をjの小さい方にとってきた)。
この時は、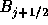 は
は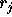 (
(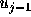 、
、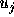 、
、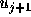 )の関数で
)の関数で

である。
しかし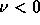 の場合は、
の場合は、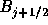 は
は
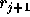 (
(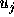 、
、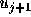 、
、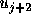 )の関数で
)の関数で
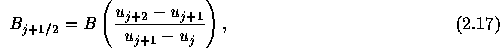
であることに注意しなければならない。
つまり、ステンシル(差分に用いる点例えばjの時間推進した値を得るために
j-1、j、j+1を使うといった差分の代表値同士の関係)が
 の正負によって変化するということに注意しなければならない。
の正負によって変化するということに注意しなければならない。