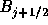前節で見た高精度風上差分についてその計算例を見てみよう。
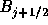について、minmod関数（図2.2）をとると
プログラムのおおよそは以下のとおりとなる。
begin
for j:=1 to jm-1 do
f[j]:=u[j]+0.5*(1-nu)*minmod(u[j]-u[j-1],u[j+1]-u[j])*(u[j+1]-u[j]);
f[0]:=f[1];
for j:=1 to jm-1 do
u[j]:=u[j]-nu*(f[j]-f[j-1]);
end;
ここで、数値流束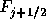
は配列f[j]に格納されており、
ながれはx軸の正の方向に向いているとして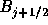
に現れる
ステンシルを固定している。
図2.2のminmod関数はプログラムでは
function minmod(d1,d2: real):real;
begin
if (d1*d2<=0) then
result:=0.0
else if (d1/d2<=1) then
result:=d1/d2
else
result:=1.0
end;
のように表される。流束制限関数をsuperbee関数に変えるには、
以下の関数を用いれば良い。
function superbee(d1,d2: real):real;
begin
if (d1*d2<=0) then
result:=0.0
else if (d1/d2<=0.5) then
result:=2*d1/d2
else if (d1/d2<=1) then
result:=1.0
else if (d1/d2<=2) then
result:=d1/d2
else
result:=2.0
end;
これらを使って、図1.2と同じ計算を行なった例をつぎの図に
示す。これをみると、流束制限関数が効いて不要な振動が押えられるとともに
かなり小さいクーラン数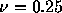
をとっても、
空間１次精度スキームのような飛びの鈍りも押えられていることがわかる。
superbee関数の方がシャープな結果を得るが、スキームの安定性では
minmod関数が勝っているといわれている。
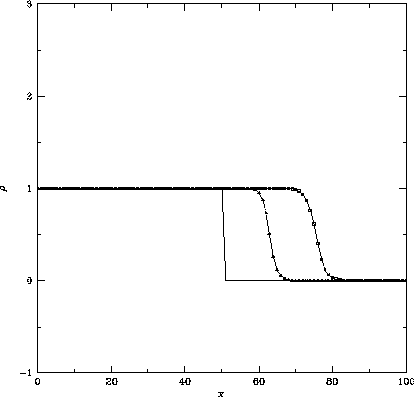
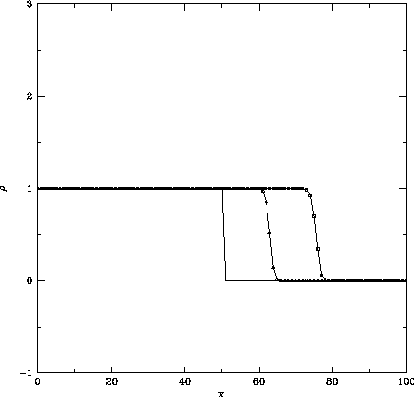
Figure 2.3: 代表的な流束制限関数を用いてadvection問題を解いた結果。
minmod関数（左）、superbee関数（右）を用いて、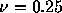
で50、100
ステップ時間を進めた結果を示している。