
で、v=c=constを考える。
流体の基礎方程式の差分法による解析に進む前に、 しばらくは、この線形の方程式に関する差分法による解析についてみてゆく。 この方程式に関する差分法による解析は、後に、流体の基礎方程式の 高精度風上差分法を構築する上での基礎となるので、しばらくつき合って いただきたい。
時間前進差分・空間中心差分の FTCS(Forward in Time and Central Difference in Space)スキームは、 式(1.24)を
のように差分化して
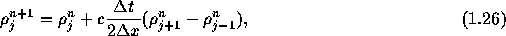
として解く方法である。 Pascalのプログラムでは
for j:=0 to jm do w[j]:=u[j]; for j:=1 to jm-1 do u[j]:=w[j]-nu/2*(w[j+1]-w[j-1]);のよう書けば良い。
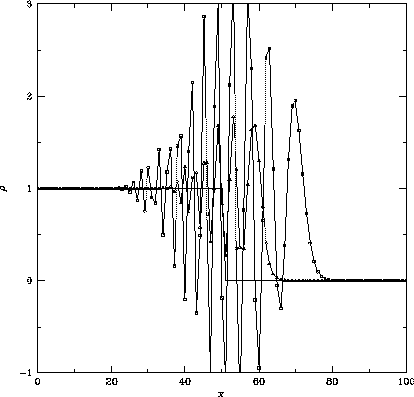
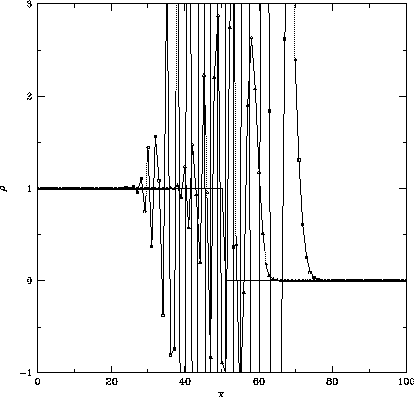
Figure 1.2: FTCSスキームで、初期値として、
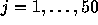 に対して
に対して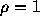 、
、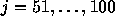 に対して
に対して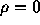 とし
クーラン数
とし
クーラン数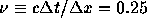 で50ステップ、100ステップ計算した
時の
で50ステップ、100ステップ計算した
時の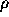 をプロットした(左)。
同じ初期条件で、クーラン数
をプロットした(左)。
同じ初期条件で、クーラン数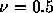 で25ステップ、50ステップ計算した
ものが右図である。
で25ステップ、50ステップ計算した
ものが右図である。
このスキームで、初期値として、
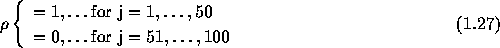
をとり、クーラン数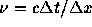 を0.25と0.5の場合について
を0.25と0.5の場合について
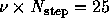 まで計算した結果が図1.2に示してある。
この初期条件に合致する厳密解は、密度が1から0へ飛ぶ位置が、
1ステップごとに右に
まで計算した結果が図1.2に示してある。
この初期条件に合致する厳密解は、密度が1から0へ飛ぶ位置が、
1ステップごとに右に だけ移動してゆくものにならなければならない
ことは容易にわかるだろう。
しかし、図1.2に示したように、このFTCSスキームを用いて
計算すると、厳密解の回りに余分の振動が発生してしまうことがわかる。
だけ移動してゆくものにならなければならない
ことは容易にわかるだろう。
しかし、図1.2に示したように、このFTCSスキームを用いて
計算すると、厳密解の回りに余分の振動が発生してしまうことがわかる。
この差分化にどれくらいの誤差が混入しているかを考える。 時間方向にテイラー展開して、
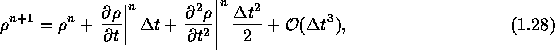
また空間方向にテイラー展開して、
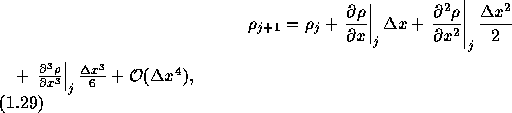
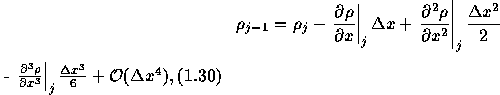
となる。 これを(1.25)に代入すると、(1.23)と完全に同じになるわけではなく、
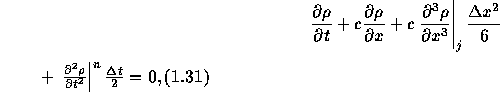
となる。
このように、空間方向に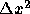 、
時間方向に
、
時間方向に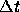 の誤差を含むスキームを、
空間2次精度、時間1次精度のスキームと呼ぶ。
の誤差を含むスキームを、
空間2次精度、時間1次精度のスキームと呼ぶ。
このFTCSスキームは図1.2に見えるように、正しい解の回りで
振動を生じており、実際に使うことはできない。
そこで、式(1.25)の右辺第1項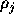 を
を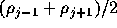 で置き換えた式
で置き換えた式
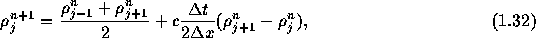
を解く方法がLax法(図1.3)である。 この方法のプログラムは
for j:=0 to jm do w[j]:=u[j]; for j:=1 to jm-1 do u[j]:=(w[j-1]+w[j+1])/2-nu/2*(w[j+1]-w[j-1]);のように書けば良い。 FTCSスキームの数値的振動は押えられているが、密度の飛びは著しく鈍ってしまって いる。
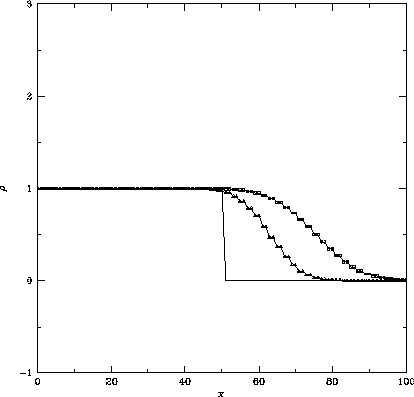
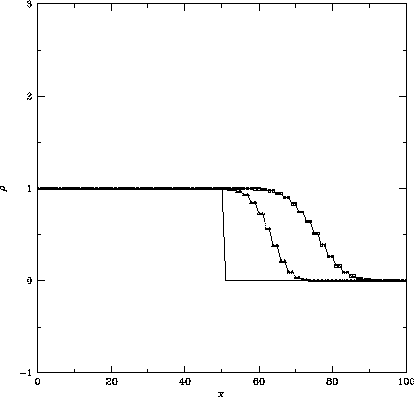
Figure: 図1.2とおなじ。ただし採用した計算スキームはLax法
で、
左はクーラン数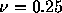 、
右はクーラン数
、
右はクーラン数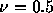 のもの。
FTCSスキームに比べて、振動はおさえられているが、密度の飛びは鈍っている。
のもの。
FTCSスキームに比べて、振動はおさえられているが、密度の飛びは鈍っている。
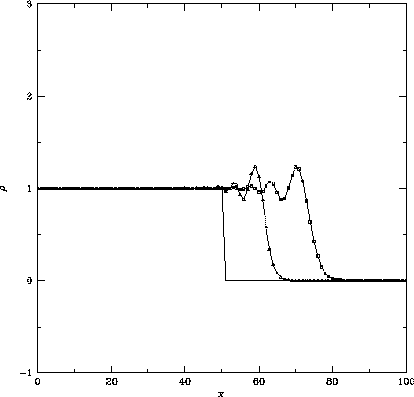
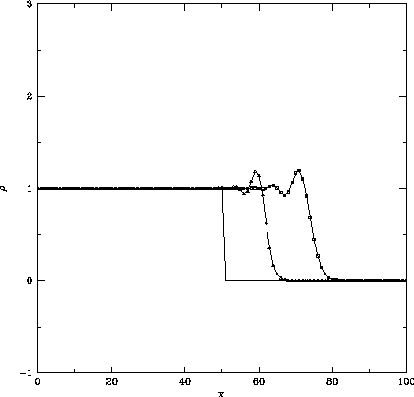
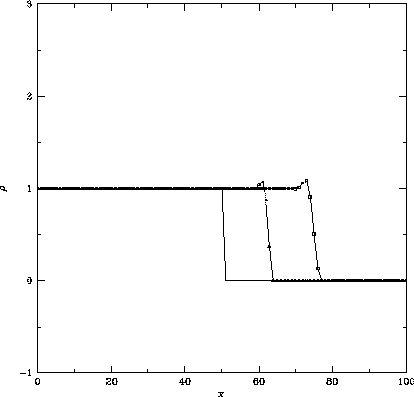
Figure 1.4: 図1.2とおなじ。ただし採用した計算スキームは
オリジナルのLax-Wendroff法で、
左はクーラン数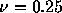 で50ステップ、100ステップ後、
中央はクーラン数
で50ステップ、100ステップ後、
中央はクーラン数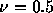 で25ステップ、50ステップ後、
右はクーラン数
で25ステップ、50ステップ後、
右はクーラン数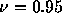 で13ステップ、26ステップ計算したもの。
で13ステップ、26ステップ計算したもの。
時間2次精度のスキームとするためには、
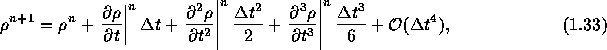
で、

であることに注すると、
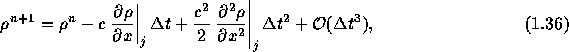
となる。この式を差分化すると オリジナルのLax-Wendroffスキームが得られる。
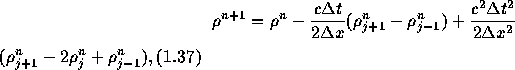
これはFTCSスキームに第3項の拡散項を加えたものとなっている。 拡散項は、FTCSスキームで生じる振動を拡散によって鎮める効果を持つので このスキームはより安定化されることになる。 プログラムは
for j:=0 to jm do w[j]:=u[j]; for j:=1 to jm-1 do u[j]:=w[j]-nu/2*(w[j+1]-w[j-1])+nu*nu/2*(w[j+1]-2*w[j]+w[j-1]);とすれば良い。