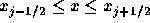セルの境界での物理量をセルの中央でのそれから内挿する方法を
考える。
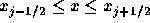に対して、物理量を
物理量uを内挿する。
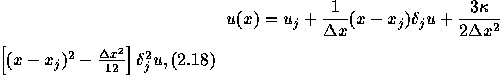
ただし、
である。
右辺第３項で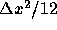
という項がつくのは、
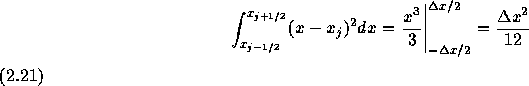
であるから、この区間について、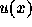
を積分して得た平均値と、
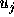を等しくするためである。
このように区分多項式で近似したときの、
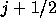での値は、左つまりj側から補間すると、
右つまりj+1側から補間すると、
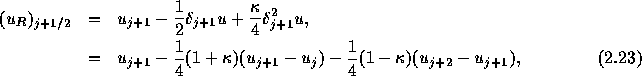
この表式は
の値によって、異なった精度の内挿公式となっている。
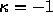とすると、
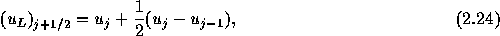
であるが、これから
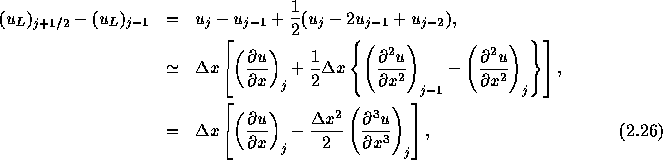
であるから、この表式は空間２次精度になっていることがわかる。
従って、左から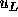
を外挿して得るのに適した風上の３点
（j-2、j-1、j）を使ってできる２次の完全風上差分
(2nd-order fully upwind)となっていることがわかる。
また、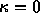
とすると、
となる。これが空間２次精度になっていることは誤差が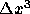
となって
いることからわかり、式(2.27)が左側から内挿したときに、
風上側３点j-2、j-1、jと
風下側１点j+1をつかって表した２次精度の風上重点差分(2nd-order upwind
biased)
であることがわかる。
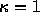とすると、式(2.22)は
のように境界での値はその中央での値の算術平均に一致する。
