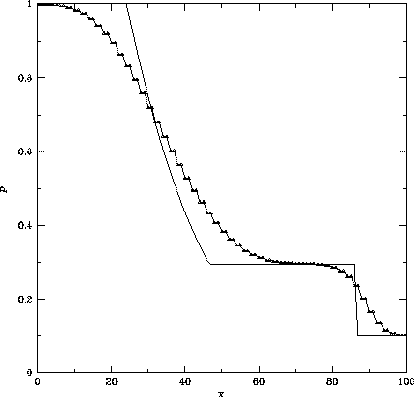
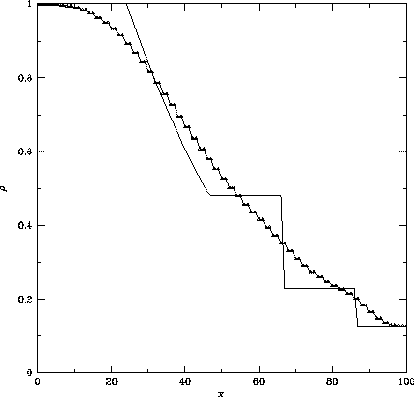
Figure 3.1: Lax法による計算例。左:圧力、右:密度分布


Figure 3.1: Lax法による計算例。左:圧力、右:密度分布
図3.1にLax法で計算した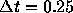 で
で
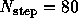 ステップ計算したのちt=20の構造を示した。
Lax法は
ステップ計算したのちt=20の構造を示した。
Lax法は

を
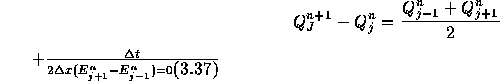
のように差分化する。これはプログラムでは
for j:=1 to jm-1 do
begin
rhon[j]:=(rho[j-1]+rho[j+1])/2-nu/2*(m[j+1]-m[j-1]);
mn[j]:=(m[j-1]+m[j+1])/2-nu/2*(gam1*(e[j+1]-e[j-1])
+gam3/2*(Sqr(m[j+1])/rho[j+1]-Sqr(m[j-1])/rho[j-1]));
en[j]:= (e[j-1]+e[j+1])/2-nu/2*(gamma*(e[j+1]*m[j+1]/rho[j+1]
-e[j-1]*m[j-1]/rho[j-1])
-gam1/2*(sqr(m[j+1]/rho[j+1])*m[j+1]
-sqr(m[j-1]/rho[j-1])*m[j-1]))
end;
のように書ける。rhon[j]は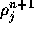 のようにnのついた量は新しい
n+1での保存量を表す。
のようにnのついた量は新しい
n+1での保存量を表す。
衝撃波面、接触不連続面ともに飛びのシャープさが全く失われている ことがわかる。また、希薄波の部分でも密度、圧力分布とも解析解と かなり異なったものとなっている。