２段階Lax-Wendroff法

先のプログラム例で計算時間を要する部分は、略されているAEの評価を行なって いる部分である。 この評価を行なわない方法がRichtmeyerによって考案された。

これは線形の問題に関しては先のオリジナルのLax-Wendroff法と同じ解を与える。 先の線形の問題では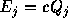であることに注意すると、 第１段階は

で、これを第２段階の式に代入すると、

となり、オリジナルのLax-Wendroff法に一致する。 ただし、非線形の問題ではLeading oriderの誤差の分だけ異なる。 プログラムは簡単になって、

  for j:=0 to jm-1 do
  begin
    rhon[j]:=(rho[j]+rho[j+1])/2-nu/2*(m[j+1]-m[j]);
    mn[j]:=(m[j]+m[j+1])/2-nu/2*(gam1*(e[j+1]-e[j])
                                 +gam3/2*(Sqr(m[j+1])/rho[j+1]-Sqr(m[j])/rho[j]));
    en[j]:= (e[j]+e[j+1])/2-nu/2*(gamma*(e[j+1]*m[j+1]/rho[j+1]
                                             -e[j]*m[j]/rho[j])
                                  -gam1/2*(sqr(m[j+1]/rho[j+1])*m[j+1]
                                          -sqr(m[j]/rho[j])*m[j]))
  end;
  rhon[jm]:=rhon[jm-1];mn[jm]:=mn[jm-1];en[jm]:=en[jm-1];

  for j:=1 to jm do
  begin
    rho[j]:=rho[j]-nu*(mn[j]-mn[j-1]);
    m[j]:=m[j]-nu*(gam1*(en[j]-en[j-1])
                     +gam3/2*(Sqr(mn[j])/rhon[j]-Sqr(mn[j-1])/rhon[j-1]));
    e[j]:=e[j]-nu*(gamma*(en[j]*mn[j]/rhon[j]-en[j-1]*mn[j-1]/rhon[j-1])
                                  -gam1/2*(sqr(mn[j]/rhon[j])*mn[j]
                                          -sqr(mn[j]/rhon[j-1])*mn[j-1]))
  end;
  rho[0]:=rho[1];m[0]:=m[1];e[0]:=e[1];

図3.2と3.3 は同じ問題をオリジナルのLax-Wendroff法を２段階のLax-Wendroff法で解いた結 果である。 衝撃波面の後ろと、接触不連続面の位置に数値的な振動が見られるが、衝撃波面や 接触不連続面の飛びが時間的に鈍ってゆくことは押えられている。

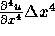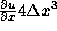Lax-Wendroff法では、数値的な振動を押える効果を持つ拡散項は、 打ち切り誤差のリーディングオーダであるではなく （この項は分散性は持つが拡散性は持たない）、次のオーダの量である の項である。 このため、差分に伴ってスキームに含まれる打ち切り誤差としての拡散項だけで は安定化に不十分な場合は、陽にこの項を方程式に付け加えて安定化をはかる 必要がある場合がある。これを陽的人工粘性項という。 ３次オーダーの４階微分項を付け加える場合、 ２段階のLax-Wendroff法では式(3.41)は

式(3.42)は

となる。 ただし、

で、kは0-1の数係数である。 この結果を図3.4に掲げる。 図3.3と比べると、衝撃波面後方および 接触不連続面近傍での振動が押えられていることがわかる。

  
Figure 3.4: 人工粘性項を付加した２段階Lax-Wendroff法による計算例。左：圧力、右：密度分布