ここでは流体力学の多次元問題を時間分割法を用いて取り扱う方法を のべる。 流体力学の方程式は、
である。例えばLax-Wendroff法について考えれば、
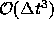を無視すると、
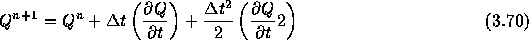
で１次元と同じように流束ヤコビアンAとBを使って、
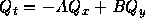、また
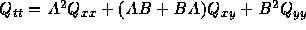である
ことに注意すると、
となることがわかる。
ここで、時間分割法は、これを
と
との連続した２つの１次元の方程式の解法に分解するものである。 ただし、このままで式(3.72)を(3.77) に代入すると、
式(3.71)と同じにはならない。 これは流束ヤコビアン（行列）AとBが可換ではない
ために発生する現象である。 これを避けるには、 分ステップを４分割して、その順序を回転させれば良い。すなわち、
とすればよい。ここで、式(3.77)と(3.78)は １つの
とすれば良いことは明らかであろう。
分ステップのオペレータを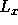
のように書くと、
のように書ける。このように書くと、１ステップ進むのに、３分ステップの
計算が必要なように見えるが、もし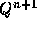
の値が必要でないなら、
直前の
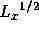は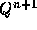
の直後に出てくる
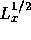と一緒に計算して
のように計算すれば良い。 これは３次元にすると、
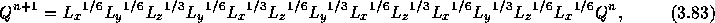
のようにすれば良いことになる。
