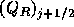 と
と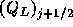 を得るところまでは
同じである。
を得るところまでは
同じである。
FVS法についても、
基本量をMUSCLで内挿して、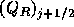 と
と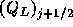 を得るところまでは
同じである。
を得るところまでは
同じである。
数値流束を計算する時(式3.59)に
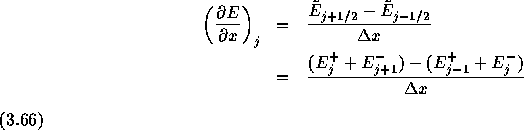
ではなく
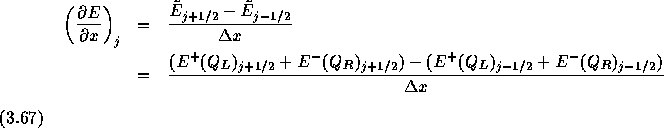
に高精度化する。
プログラムでは
E1p[j]:=w[1,1]*rhoL[j]+w[1,2]*mL[j]+w[1,3]*eL[j];
E2p[j]:=w[2,1]*rhoL[j]+w[2,2]*mL[j]+w[2,3]*eL[j];
E3p[j]:=w[3,1]*rhoL[j]+w[3,2]*mL[j]+w[3,3]*eL[j];
....
E1m[j]:=w[1,1]*rhoR[j]+w[1,2]*mR[j]+w[1,3]*eR[j];
E2m[j]:=w[2,1]*rhoR[j]+w[2,2]*mR[j]+w[2,3]*eR[j];
E3m[j]:=w[3,1]*rhoR[j]+w[3,2]*mR[j]+w[3,3]*eR[j];
のようになる。
これを用いてテスト問題を計算した結果を図3.9に掲げる。 MUSCLで2次精度化したFDS法と同様に、衝撃波面の後ろ側の振動もほとんど押えられ、 接触不連続面や衝撃波面が時間的に鈍ってゆくことも空間1次精度の 図3.7に比べて改善されていることがわかる。
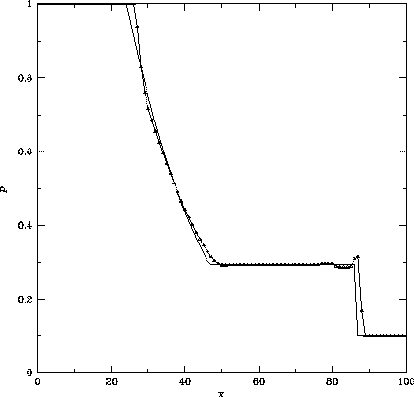
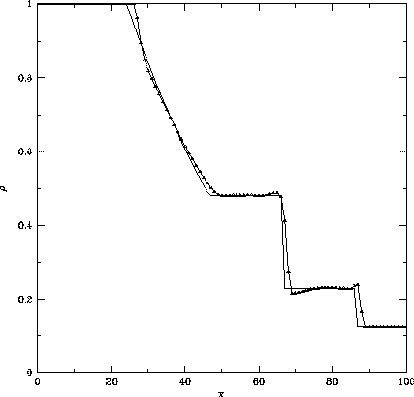
Figure 3.9: MUSCLで2次精度化したFlux Vector Splitting法による衝撃波管問題の解。
初期条件は同じ。