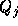差分

空間微分の差分化を考える。 空間を格子に分割しその格子点上の物理量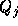を計算する。 ここでjは格子点につけた番号を表す。

この３つの表現は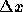が小さい極限ではおなじ 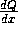を与えるが、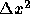のオーダで違う量を与える （詳しくは後に述べる）。 式(1.15)のようにとるのを前進差分、 式(1.16)のようにとるのを後退差分、 式(1.17)のようにとるのを中心差分と呼ぶ。

どのような差分をとるかということは、計算方法の安定性、収束性などに 影響を与える。 これはこの授業の主要な内容にあたる。