陽解法と陰解法

式(1.12)

を時間について差分化する方法も、前進、後退、中心差分を考えることができる。 時間に関する添字をnとし、nステップめの物理量からn+1ステップめの それを求める（時間進化を求める）ことを考える。 これが流体力学の非定常問題の解を求めることに相当している。

時間に関しては前進差分、中心差分そして後退差分を適用すると、それぞれ

のようになる。 ここで、前の２つは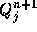を求めるのに、過去の情報 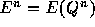や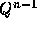のみを使っている。 したがって既に知れている情報で求める１つ時間ステップ進んだ後の 物理量の値を決めることができる。 このようにな方法を陽解法と呼ぶ。 それに対して、式(1.21)では、 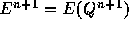だから、１つ時間ステップ進んだ後の物理量の値を決めるのに、 それを右辺に含んでいる。 このような解法は陰解法とよばれ、１つ時間ステップ進んだ後の物理量の値を決める のに、それら自身の間にある関係を使わなければならないことになっている。 具体的には、陰解法では、空間の格子点数従属変数の種類だけの変数に関する 連立方程式を１ステップごとに解く必要がある。