



Next: Energy Equation from the
Up: Energy Equation
Previous: Energy Equation
Contents
If the pressure of the fluid, 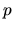 , is expressed only by the density,
, is expressed only by the density, 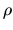 ,
,
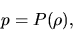 |
(A.17) |
the number of dependent variables is reduced to two and the above equations are sufficient
to describe the dynamics of the fluid.
Occasionally, the presure is assumed proportional to the power of 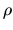 as
as
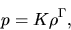 |
(A.18) |
where 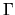 is a constant.
This assumption is called polytropic relation.
is a constant.
This assumption is called polytropic relation.
The fact should be reminded that the validity of the assumption comes from the physical condition of the system.
In the case that the temperature of the gas is kept constant owing to the cooling and heating process,
the gas pressure is proportional to the density
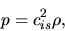 |
(A.19) |
where
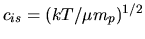 (
(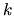 : Boltzmann constant,
: Boltzmann constant, 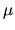 average molecular weight, and
average molecular weight, and
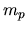 is the proton mass) represents the isothermal sound speed and is constant.
is the proton mass) represents the isothermal sound speed and is constant.
Another example is the isentropic fluid, in which the entropy is kept constant.
In this case the pressure is proportional to 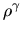 , as
, as
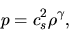 |
(A.20) |
where 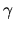 is the specific heat ratio
is the specific heat ratio 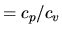 and
and
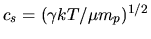 represents the adiabatic sound speed.
In these cases the polytropic replations of equations (A.19) and
(A.20) plays a role as the third equation of basic equations of hydrodynamics.
represents the adiabatic sound speed.
In these cases the polytropic replations of equations (A.19) and
(A.20) plays a role as the third equation of basic equations of hydrodynamics.




Next: Energy Equation from the
Up: Energy Equation
Previous: Energy Equation
Contents
Kohji Tomisaka
2007-07-08
![]() , is expressed only by the density,
, is expressed only by the density, ![]() ,
,
![]() , as
, as