



Next: Shock Wave
Up: Energy Equation
Previous: Polytropic Relation
Contents
In more general cases, the last equation comes from the first law of the thermal physics,
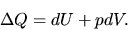 |
(A.21) |
where 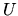 and
and 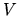 represent the internal energy and the volume and
represent the internal energy and the volume and 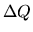 is the heat
added or subtracted from the system.
Using the total energy per unit volume
is the heat
added or subtracted from the system.
Using the total energy per unit volume
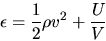 |
(A.22) |
the above equation gives the equation for total energy:
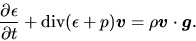 |
(A.23) |
Since the total energy per unit volume is expressed using the basic physical quantities as
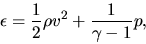 |
(A.24) |
equation (A.23) is the final basic equation for hydrodynamics.
Equations (A.7), (A.11), and (A.23)
are basic equations hydrodynamics using the Eulerian time derivative.
Problem:
From the continuity equation (A.11) and
the equation of motion (A.7) or
the equation for momentum density (A.15),
show that the equation for the kinetic enerygy density
is expressed as follows
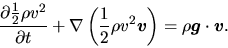 |
(A.25) |
Then, obtain equation for the total energy (A.23).




Next: Shock Wave
Up: Energy Equation
Previous: Polytropic Relation
Contents
Kohji Tomisaka
2007-07-08