



Next: Physical Background
Up: Introduction
Previous: Mass Spectrum
Contents
Larson (1981) compiled the observations for molecular cloud complexes,
molecular cloud and molecular clumps published in 1974-1979.
He obtained an empirical relation
that the size of a structure is well correlated
to the random velocity in the structure which is measured by the
width of the emission line (see Appendix E).
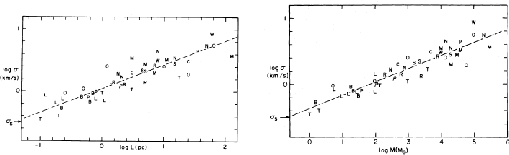
Figure 1.28(left) shows this correlation and this is well expressed
as
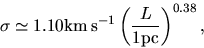 |
(1.13) |
where 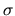 and
and 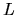 represent respectively
the three-dimensional random speed of gas and the size of the structure.
A similar correlation is found only for giant molecular clouds
(Sanders, Scoville, & Solomon 1985) as
represent respectively
the three-dimensional random speed of gas and the size of the structure.
A similar correlation is found only for giant molecular clouds
(Sanders, Scoville, & Solomon 1985) as
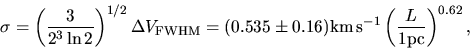 |
(1.14) |
for GMCs whose sizes are larger than 10pc (be careful the typos in their
abstract: power was -0.62).
He also found another correlation between the mass 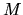 and the random velocity
like Figure 1.28(right), which is expressed as
and the random velocity
like Figure 1.28(right), which is expressed as
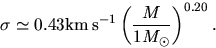 |
(1.15) |
In the next chapter ( 2.9), we will see
the virial relation, that is, for an isolated system to achieve
a mechanical equlibrium the gravitaional to thermal energy ratio has
to be equal to 2:1 for
2.9), we will see
the virial relation, that is, for an isolated system to achieve
a mechanical equlibrium the gravitaional to thermal energy ratio has
to be equal to 2:1 for 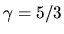 gas.
The ratio of the gravitational energy
gas.
The ratio of the gravitational energy
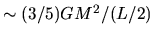 to the thermal energy
to the thermal energy 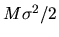 is also fitted as
is also fitted as
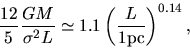 |
(1.16) |
which is weakly dependent of the size or the mass.
This seems to mean the ratio is nearly
constant irrespective of the mass or size of the clouds.
Since there is a mutual relation between mass, size, and the velocity
dispersion to achive a mechanical equlibrium (the Virial relation),
there is only one independent correlation in the above two
correlations (eqs.[1.13] and [1.15]).
Although several reasons to explain the correlation are proposed,
we have no consensus yet.
Figure 1.28:
The left shows the relation between cloud size (holizontal axis)
and the three-dimensional internal velocity (vertical axis).
The right shows a similar correlation between mass and the random velocity.
 |




Next: Physical Background
Up: Introduction
Previous: Mass Spectrum
Contents
Kohji Tomisaka
2007-07-08
