



Next: Steady State Flow under
Up: Super- and Subsonic Flow
Previous: Super- and Subsonic Flow
Contents
Flow in the Laval Nozzle
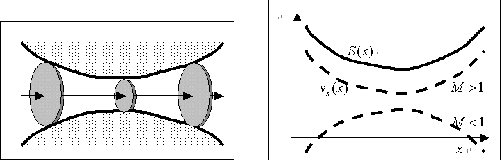
Figure 2.5:
Left: Explanation of Laval nozzle. Right: The relation between the cross-section 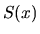 and the flow velocity
and the flow velocity 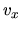 .
.
 |
Consider a tube whose cross-section, 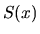 , changes gradually, which is called Laval nozzle.
Assuming the flow is steady
, changes gradually, which is called Laval nozzle.
Assuming the flow is steady
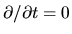 and is essentially one-dimensional,
the continuity equation (2.1) is rewritten as
and is essentially one-dimensional,
the continuity equation (2.1) is rewritten as
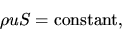 |
(2.85) |
or
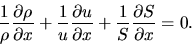 |
(2.86) |
Equation of motion (2.2) becomes
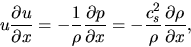 |
(2.87) |
where we used the relationship of
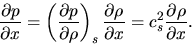 |
(2.88) |
When the flow is isothermal, use the isothermal sound speed 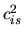 instead of the adiabatic one.
From equations (2.86) and (2.87),
we obtain
instead of the adiabatic one.
From equations (2.86) and (2.87),
we obtain
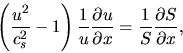 |
(2.89) |
where the factor
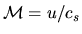 is called the Mach number.
For supersonic flow
is called the Mach number.
For supersonic flow 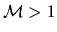 , while
, while 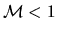 for subsonic flow.
for subsonic flow.
In the supersonic regime 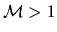 ,
the factor in the parenthesis of the lhs of equation (2.88) is positive.
This leads to the fact that the velocity increases (
,
the factor in the parenthesis of the lhs of equation (2.88) is positive.
This leads to the fact that the velocity increases (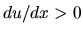 ) as long as the cross-section increases (
) as long as the cross-section increases (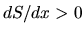 ).
On the other hand, in the subsonic regime, the velocity decreases (
).
On the other hand, in the subsonic regime, the velocity decreases (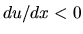 )
while the cross-section increases (
)
while the cross-section increases (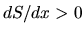 ).
See right panel of 2.5.
).
See right panel of 2.5.
If 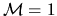 at the point of minimum cross-section (throat), two curves for
at the point of minimum cross-section (throat), two curves for 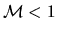 and
and 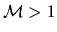 have an
intersection.
In this case, gas can be accelerated through the Laval nozzle.
First, a subsonic flow is accelerated to the sonic speed at the throat of the nozzle.
After passing the throat, the gas follows the path of a supersonic flow, where the velocity is accelerated as long as
the cross-section increases.
have an
intersection.
In this case, gas can be accelerated through the Laval nozzle.
First, a subsonic flow is accelerated to the sonic speed at the throat of the nozzle.
After passing the throat, the gas follows the path of a supersonic flow, where the velocity is accelerated as long as
the cross-section increases.




Next: Steady State Flow under
Up: Super- and Subsonic Flow
Previous: Super- and Subsonic Flow
Contents
Kohji Tomisaka
2007-07-08


![]() ,
the factor in the parenthesis of the lhs of equation (2.88) is positive.
This leads to the fact that the velocity increases (
,
the factor in the parenthesis of the lhs of equation (2.88) is positive.
This leads to the fact that the velocity increases (![]() ) as long as the cross-section increases (
) as long as the cross-section increases (![]() ).
On the other hand, in the subsonic regime, the velocity decreases (
).
On the other hand, in the subsonic regime, the velocity decreases (![]() )
while the cross-section increases (
)
while the cross-section increases (![]() ).
See right panel of 2.5.
).
See right panel of 2.5.
![]() at the point of minimum cross-section (throat), two curves for
at the point of minimum cross-section (throat), two curves for ![]() and
and ![]() have an
intersection.
In this case, gas can be accelerated through the Laval nozzle.
First, a subsonic flow is accelerated to the sonic speed at the throat of the nozzle.
After passing the throat, the gas follows the path of a supersonic flow, where the velocity is accelerated as long as
the cross-section increases.
have an
intersection.
In this case, gas can be accelerated through the Laval nozzle.
First, a subsonic flow is accelerated to the sonic speed at the throat of the nozzle.
After passing the throat, the gas follows the path of a supersonic flow, where the velocity is accelerated as long as
the cross-section increases.