 |
 |
Consider a flow under a force exerted on the gas whose strength varies spatially.
Let ![]() represent the force working per unit mass.
Assuming the cross-section is constant
represent the force working per unit mass.
Assuming the cross-section is constant
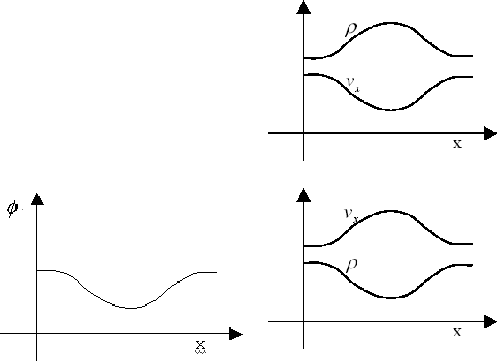
Consider an external field whose potential is shown in Figure 2.6(Left).
(1) For subsonic flow, the factor in the parenthesis is negative.
Before the potential minimum, since ![]() ,
, ![]() is decelerated.
On th other hand, after the potential minimum,
is decelerated.
On th other hand, after the potential minimum, ![]() is accelerated owing to
is accelerated owing to ![]() .
Using equation (2.90), this leads to a density distribution in which density peaks near the potential minimum.
(2) For supersonic flow, the factor is positive.
In the region of
.
Using equation (2.90), this leads to a density distribution in which density peaks near the potential minimum.
(2) For supersonic flow, the factor is positive.
In the region of ![]() ,
, ![]() is accelerated.
After passing the potential minimum,
is accelerated.
After passing the potential minimum, ![]() is decelerated.
The velocity and the density distribution is shown in Figure 2.6(right-lower panel).
is decelerated.
The velocity and the density distribution is shown in Figure 2.6(right-lower panel).
The density distribution of the subsonic flow in an external potential is similar to that of hydrostatic one. That is, considering the hydrostatic state in an external potential, the gas density peaks at the potential minimum. On the other hand, The density distribution of the supersonic flow looks like that made by ballistic particles which are moving freely in the potential. Owing to the conservation of the total energy (kinetic + potential energies), the velocity peaks at the potential minimum. And the condition of mass conservation leads to the distribution in which the density decreases near the potential minimum.