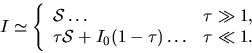Next: Einstein's Coefficients
Up: Radiative Transfer
Previous: Radiative Transfer
Contents
Radiative Transfer Equation
Specific intensity of radiation fields
 is defined by
the radiation energy
is defined by
the radiation energy  transferred by photons with wavelength
transferred by photons with wavelength  through a unit surface placed at
through a unit surface placed at
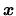 whose normal is directed to
whose normal is directed to
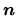 per unit time per unit wavelength, and per unit steradian.
Average intensity of radiation
per unit time per unit wavelength, and per unit steradian.
Average intensity of radiation
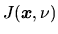 is defined as
is defined as
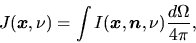 |
(2.121) |
where 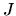 is obtained by averaging
is obtained by averaging 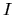 for the solid angle.
This is related to the energy density of radiation
for the solid angle.
This is related to the energy density of radiation
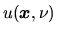 as
as
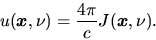 |
(2.122) |
If the radiation is absorbed in the displacement 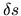 as
as
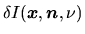 ,
,
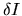 must be proportional to
must be proportional to 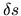 and
and
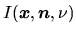 as
as
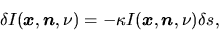 |
(2.123) |
where 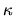 is a coefficient and called volume absorption coefficient.
The dimension of
is a coefficient and called volume absorption coefficient.
The dimension of 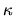 is
is 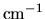 .
We can rewrite the above to the differential equation as
.
We can rewrite the above to the differential equation as
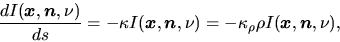 |
(2.124) |
where we used mass absorption coefficient 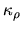 which represents
the absorption per mass.
Equation (2.123) is reduced to
which represents
the absorption per mass.
Equation (2.123) is reduced to
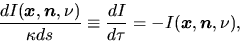 |
(2.125) |
where
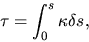 |
(2.126) |
is called the optical depth.
This means that 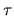 is a measure for absorption as
the intensity decreases at a factor
is a measure for absorption as
the intensity decreases at a factor 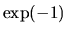 from
from 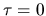 to
to 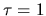 .
.
If the ray runs  crossing a volume whose
volume emissivity equal to
crossing a volume whose
volume emissivity equal to  the intensity increases
the intensity increases
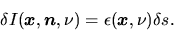 |
(2.127) |
The volume emissivity
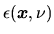 is the energy
emitted by a unit volume at a position
is the energy
emitted by a unit volume at a position
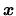 per unit time
per unit solid angle per unit wavelength.
From equations (2.123) and (2.127),
the radiation transfer is written as
per unit time
per unit solid angle per unit wavelength.
From equations (2.123) and (2.127),
the radiation transfer is written as
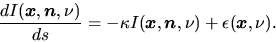 |
(2.128) |
Using the optical denpth
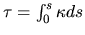 ,
this gives
,
this gives
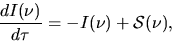 |
(2.129) |
where 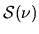 is called the source function and is defined as
is called the source function and is defined as
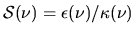 .
Assuming the specific intensity
.
Assuming the specific intensity 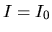 at the point of
at the point of 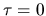 ,
that at the point
,
that at the point 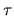 on the same ray is given
on the same ray is given
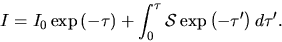 |
(2.130) |
In the case of constant source term 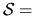 const it reduces to
const it reduces to
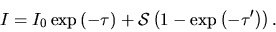 |
(2.131) |
Equation (2.130) gives
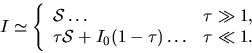 |
(2.132) |
This indicates that if we see an optically thick cloud
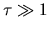 the specific intensity reaches us represents
the specific intensity reaches us represents 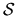 ,
while if we see an transparent cloud
,
while if we see an transparent cloud 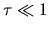 ,
, 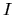 represents
that of background.
represents
that of background.
Problem
Show that
equations (2.130) and (2.130)
are solutions of equation (2.129).




Next: Einstein's Coefficients
Up: Radiative Transfer
Previous: Radiative Transfer
Contents
Kohji Tomisaka
2007-07-08
![]() as
as
![]() ,
,
![]() must be proportional to
must be proportional to ![]() and
and
![]() as
as
![]() crossing a volume whose
volume emissivity equal to
crossing a volume whose
volume emissivity equal to ![]() the intensity increases
the intensity increases