



Next: Group Velocity
Up: Galactic Scale Star Formation
Previous: Spiral Structure
Contents
Density Wave Theory
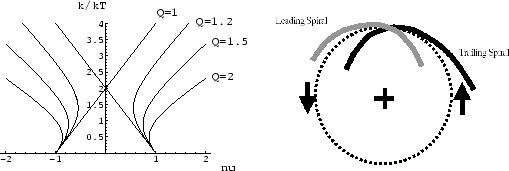
Figure 3.7:
(Left:) A plot of the dispersion relation eq.(2.65).
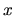 - and
- and 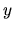 -axes are
-axes are 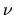 and
and 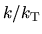 .
Respective lines are for
.
Respective lines are for 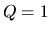 (straight lines),
(straight lines), 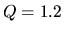 ,
, 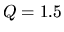 , and
, and 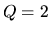 .
The trailing part
.
The trailing part 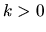 is only plotted.
Points
is only plotted.
Points 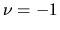 ,
, 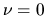 , and
, and 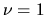 correspond respectively to Inner Lindbrad Resonance (ILR),
Corotation Resonance (CR), and Outer Lindbrad Resonance (OLR).
The relation is symmetric against the
correspond respectively to Inner Lindbrad Resonance (ILR),
Corotation Resonance (CR), and Outer Lindbrad Resonance (OLR).
The relation is symmetric against the 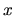 -axis and the curve of
-axis and the curve of 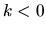 represents the leading wave.
(Right:) Leading vs trailing spiral.
represents the leading wave.
(Right:) Leading vs trailing spiral.
 |
We have derived the dispersion relation of the gravitational instability in the rotating thin disk as
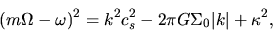 |
(3.36) |
where 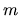 represents the number of spiral arms.
Although the stability of the stellar system is a little different,
we assume this is valid for the stellar system after
represents the number of spiral arms.
Although the stability of the stellar system is a little different,
we assume this is valid for the stellar system after 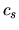 is replaced to the velocity dispersion.
Since
is replaced to the velocity dispersion.
Since
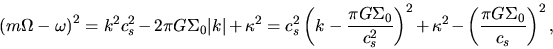 |
(3.37) |
we obtain
![\begin{displaymath}
\vert k\vert= k_{\rm T}\frac{2}{Q^2}\left[1 \pm \sqrt{1 -Q^{2}(1 - \nu^2)}\right],
\end{displaymath}](img763.png) |
(3.38) |
where
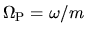 is a pattern speed,
is a pattern speed,
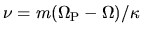 is the normalized
frequency,
is the normalized
frequency,
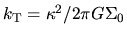 is the Toomre's critical wavenumber for a cold (
is the Toomre's critical wavenumber for a cold (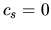 ) system.
) system.
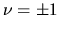 , which leads to
, which leads to 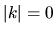 , represents the Lindbrad resonance and is rewriten as
, represents the Lindbrad resonance and is rewriten as
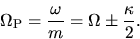 |
(3.39) |
Assuming 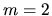 ,
the resonance when
,
the resonance when
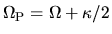 is called outer Lindbrad resonance while
that of
is called outer Lindbrad resonance while
that of
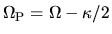 is called inner Lindbrad resonance.
is called inner Lindbrad resonance.
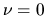 means the co-rotation resonance
means the co-rotation resonance
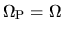 .
Plotting the wavenumber
.
Plotting the wavenumber 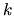 against the normalized frequency
against the normalized frequency 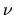 of
equation (3.38) as Figure 3.7(left),
it is shown that, in the case of
of
equation (3.38) as Figure 3.7(left),
it is shown that, in the case of 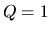 , the wavenumber exists for all
, the wavenumber exists for all 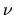 .
Since
.
Since 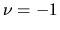 , 0, and +1 correspond to the points of ILR, CR, and OLR and these three resonance points
appear in accordance with the radial distance, the
, 0, and +1 correspond to the points of ILR, CR, and OLR and these three resonance points
appear in accordance with the radial distance, the 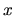 -axis of Figure 3.7(left)
seems to correspond to the radial distance from the center.
In the case of
-axis of Figure 3.7(left)
seems to correspond to the radial distance from the center.
In the case of 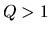 , it is shown that a forbidden region appears around the co-rotation resonance point.
Waves cannot propagate into the region.
Figure 3.7(left) shows that
the
, it is shown that a forbidden region appears around the co-rotation resonance point.
Waves cannot propagate into the region.
Figure 3.7(left) shows that
the 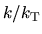 has two possible wavenumbers in the permitted region.
The waves with larger
has two possible wavenumbers in the permitted region.
The waves with larger 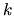 and smaller
and smaller 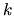 are called short waves and long waves, respectively.
Consider a wave expressed by
are called short waves and long waves, respectively.
Consider a wave expressed by
![$\Sigma \propto \exp[im\phi+ikr]$](img775.png) .
If
.
If 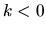 , moving from a point
, moving from a point 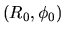 in the direction
in the direction 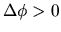 and
and 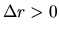 the phase difference between the two points
the phase difference between the two points
![$[m(\phi_0+ \Delta \phi) + k (R_0+\Delta r)] - [m\phi_0+k R_0]$](img778.png) can be equal to zero.
That is, in the case of
can be equal to zero.
That is, in the case of 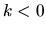 the wave is leading.
On the other hand, if
the wave is leading.
On the other hand, if 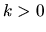 , moving in the direction
, moving in the direction 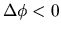 and
and 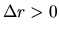 the phase
will be unchanged.
In this case, the wave pattern is trailing.
Since the dispersion relation is symmetric for
the phase
will be unchanged.
In this case, the wave pattern is trailing.
Since the dispersion relation is symmetric for 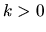 and
and 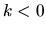 , there are two waves, trailing waves and
leading waves.
Therefore there are four waves: a short trailing wave, a long trailing wave,
a short leading wave, and a long leading wave.
, there are two waves, trailing waves and
leading waves.
Therefore there are four waves: a short trailing wave, a long trailing wave,
a short leading wave, and a long leading wave.
Subsections




Next: Group Velocity
Up: Galactic Scale Star Formation
Previous: Spiral Structure
Contents
Kohji Tomisaka
2007-07-08

