



Next: Local Star Formation Process
Up: Galactic Scale Star Formation
Previous: Group Velocity
Contents
In the preceding section, we have seen that a spiral pattern of density perturbation is made
by the gravitational instability in the stellar system with
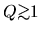 .
This forms a grand design spiral observed in the
.
This forms a grand design spiral observed in the 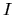 -band images which represent the mass distribution
which consists essentially in less-massive stars.
The amplitude of the pattern is smaller than that observed in
-band images which represent the mass distribution
which consists essentially in less-massive stars.
The amplitude of the pattern is smaller than that observed in 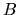 -band images.
In this section we will see how the distribution early type stars is explained.
[Recommendation for a reference book of this section: Spitzer (1978).]
-band images.
In this section we will see how the distribution early type stars is explained.
[Recommendation for a reference book of this section: Spitzer (1978).]
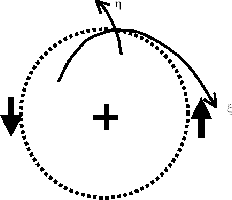
Figure 3.8:
Spiral coordinate. Along a curve of constant 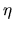 ,
,
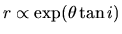 .
.
 |
Gas flowing through a spiral gravitational potential, even if its amplitude is relatively small,
acts rather nonlinearly.
Consider the gravitational potential in the sum of an axisymmetric term, 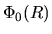 and a
spiral term
and a
spiral term 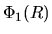 .
The spiral gravitational field is rotating with a pattern speed
.
The spiral gravitational field is rotating with a pattern speed
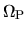 .
We use a reference frame rotating with
.
We use a reference frame rotating with
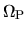 .
.
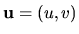 , where
, where 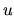 and
and 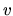 are radial (
are radial (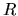 ) and azimuthal (
) and azimuthal (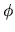 ) component of the flow velocity.
Consider the reference system rotating with the angular rotation speed
) component of the flow velocity.
Consider the reference system rotating with the angular rotation speed
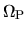 .
We assume the variables with suffix 0 represent those without the spiral potential
.
We assume the variables with suffix 0 represent those without the spiral potential 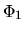 and
variables with suffix 1 are used to express the difference between before and after
and
variables with suffix 1 are used to express the difference between before and after 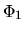 is added.
is added.
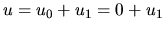 ,
, 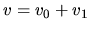 , and
, and
![\begin{displaymath}
v_0=R(\Omega-\Omega_{\rm P})=R\left[\left(\frac{1}{R}\frac{...
...ial \Phi_0}{\partial R}\right)^{1/2}-\Omega_{\rm P}\right],
\end{displaymath}](img799.png) |
(3.41) |
where 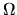 means the circular rotation speed.
The equation of motion in the
means the circular rotation speed.
The equation of motion in the 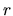 -direction is
-direction is
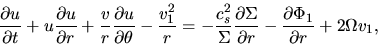 |
(3.42) |
and that in the 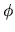 direction is
direction is
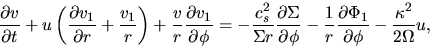 |
(3.43) |
and the continuity equation is
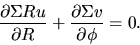 |
(3.44) |
As seen in Figure 3.8, we introduce the spiral coordinate 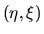 in which
in which  -axis
is parallel to the spiral pattern which has a pitch angle
-axis
is parallel to the spiral pattern which has a pitch angle 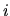 and
and 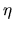 -axis is perpendicular to the
-axis is perpendicular to the 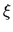 -axis.
-axis.
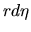 |
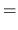 |
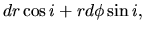 |
(3.45) |
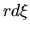 |
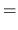 |
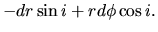 |
(3.46) |
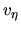 |
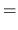 |
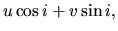 |
(3.47) |
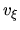 |
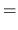 |
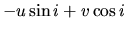 |
(3.48) |
Assuming that 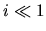 (tightly wound spiral), equations (3.44) (3.42)
and (3.43) become
(tightly wound spiral), equations (3.44) (3.42)
and (3.43) become
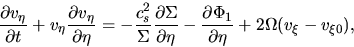 |
(3.49) |
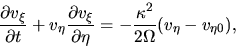 |
(3.50) |
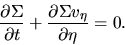 |
(3.51) |
Similar to  2.8 we look for a steady state solution.
Equation (3.51) becomes
2.8 we look for a steady state solution.
Equation (3.51) becomes
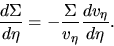 |
(3.52) |
Using this, equation (3.49) reduces to
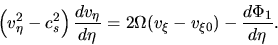 |
(3.53) |
Equation (3.50) becomes
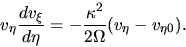 |
(3.54) |
In these equations we used following quantities:
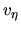 |
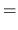 |
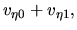 |
(3.55) |
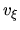 |
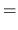 |
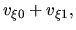 |
(3.56) |
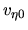 |
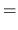 |
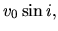 |
(3.57) |
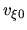 |
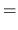 |
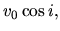 |
(3.58) |
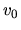 is given in equation (3.41).
Equations (3.52), (3.53), and (3.54) are solved under the periodic boundary condition:
is given in equation (3.41).
Equations (3.52), (3.53), and (3.54) are solved under the periodic boundary condition:
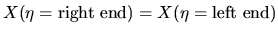 .
Since equation (3.53) is similar to the equations in
.
Since equation (3.53) is similar to the equations in  2.8,
you may think the solution seems like Figure 2.6.
However, it contains a term which expresses the effect of Coliois force
2.8,
you may think the solution seems like Figure 2.6.
However, it contains a term which expresses the effect of Coliois force
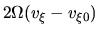 ,
the flow becomes much complicated.
Taking care of the point that a shock front exists for a range of parameters, the solution of the above equations
are shown in Figure 3.9.
Numerical hydrodynamical calculations which solve equations (3.49), (3.50), and (3.51) was done and steady state solutions are obtained (Woodward 1975).
It is shown that
,
the flow becomes much complicated.
Taking care of the point that a shock front exists for a range of parameters, the solution of the above equations
are shown in Figure 3.9.
Numerical hydrodynamical calculations which solve equations (3.49), (3.50), and (3.51) was done and steady state solutions are obtained (Woodward 1975).
It is shown that 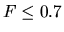 %, the velocity (
%, the velocity (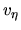 : velocity perpendicular to the wave) does not show
any discontinuity.
In contrast, for
: velocity perpendicular to the wave) does not show
any discontinuity.
In contrast, for 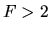 %, a shock wave appears.
Steady state solution is obtained from the ordinary differential equations (3.52)
(3.53), and (3.54) by Shu, Milione, & Roberts (1973).
Inside the CR,
%, a shock wave appears.
Steady state solution is obtained from the ordinary differential equations (3.52)
(3.53), and (3.54) by Shu, Milione, & Roberts (1973).
Inside the CR, 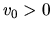 (Gas has a faster rotation speed than the spiral pattern).
As long as
(Gas has a faster rotation speed than the spiral pattern).
As long as 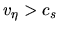 there is no shock.
Increasing the amplitude of the spiral force
there is no shock.
Increasing the amplitude of the spiral force 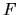 , an amplitude of the variation in
, an amplitude of the variation in 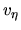 increases and finally
increases and finally
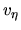 becomes subsonic partially.
When the flow changes its nature from supersonic to subsonic, it is accompanied with a shock.
(An inverse process, that is, changing from subsonic to supersonic is not accompanied with a shock.)
In the outer galaxy (still inside CR) since
becomes subsonic partially.
When the flow changes its nature from supersonic to subsonic, it is accompanied with a shock.
(An inverse process, that is, changing from subsonic to supersonic is not accompanied with a shock.)
In the outer galaxy (still inside CR) since
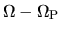 decreases with the the distance from the galactic center,
decreases with the the distance from the galactic center,
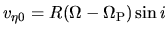 decreases.
In this region,
decreases.
In this region,
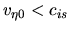 and the flow is subsonic if there is no spiral gravitational force,
and the flow is subsonic if there is no spiral gravitational force, 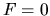 .
In such a circumstance, increasing
.
In such a circumstance, increasing 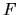 amplifies the variation in
amplifies the variation in 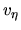 and
and 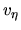 finally reaches the sound speed.
Transonic flow shows again a shock.
Summary of this section is:
finally reaches the sound speed.
Transonic flow shows again a shock.
Summary of this section is:
- There exists a spiral density pattern of the stellar component if the Toomre's
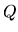 parameter is
parameter is
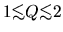 .
.
- This is driven by the self-gravity of the rotating thin disk.
- If the amplitude of the non-axisymmetric force is as large as
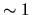 % of the axisymmetric one,
interstellar gas whose sound speed is as large as
% of the axisymmetric one,
interstellar gas whose sound speed is as large as
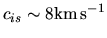 forms the galactic shock.
This is observed when the flow is transonic.
forms the galactic shock.
This is observed when the flow is transonic.
- The amplitude of the gas density fluctuation is much larger than that in the stellar density.
- If stars are formed preferentially in the postshock region of the spiral arm, we expect
clear spiral arms made by early-type stars, which are massive and short-lived,
as seen in the
 -band images of spiral galaxies.
-band images of spiral galaxies.
Figure:
Galactic shocks.
The velocity perpendicular to the spiral wave front is plotted against the phase of the spiral wave.
Gas flows from the left to the right.
The spiral potential takes its minimum at 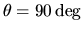 .
Parameters are taken as
.
Parameters are taken as
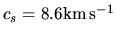 ,
, 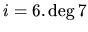 ,
, 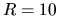 kpc,
kpc,
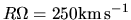 ,
,
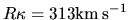 ,
,
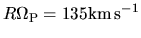 .
The amplitude of spiral gravity force is taken
.
The amplitude of spiral gravity force is taken 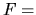 0.4%, 0.7%, 2%, and 5% of the axisymmetric force
0.4%, 0.7%, 2%, and 5% of the axisymmetric force
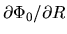 .
Taken from Fig.13.3 of Spizer (1978) [originally Woodward (1975)].
.
Taken from Fig.13.3 of Spizer (1978) [originally Woodward (1975)].
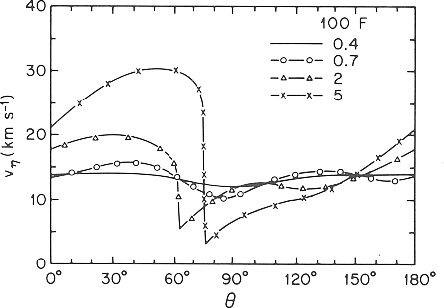 |
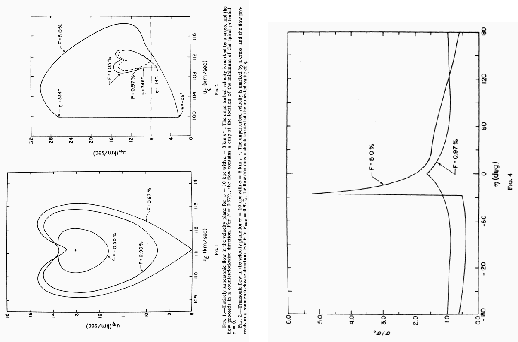
Figure 3.10:
Galactic shock.
(Left:) 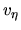 vs
vs 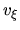 plot.
Increasing
plot.
Increasing 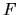 from 0.5% to 0.9%, the variation in
from 0.5% to 0.9%, the variation in 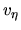 increases.
And at
increases.
And at 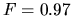 %, the minimum speed reaches the sound
speed
%, the minimum speed reaches the sound
speed
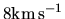 .
Further increasing
.
Further increasing 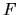 , a subsonic region appears
(
, a subsonic region appears
(
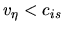 for
for 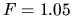 % and 5%).
When flow changes its nature from supersonic to subsonic, a shock appears.
% and 5%).
When flow changes its nature from supersonic to subsonic, a shock appears.
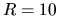 kpc,
kpc,
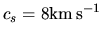 , and
, and 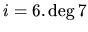 are taken.
Other parameters are the same as Fig.3.9.
(Right:) Comparison of two density distributions:
there are no shocks only cusps for
are taken.
Other parameters are the same as Fig.3.9.
(Right:) Comparison of two density distributions:
there are no shocks only cusps for 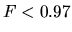 %, while
shochs and high compressions in the postshock region appear for models
with
%, while
shochs and high compressions in the postshock region appear for models
with 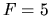 %.
Taken from Shu, Milione, & Roberts (1973).
%.
Taken from Shu, Milione, & Roberts (1973).
 |




Next: Local Star Formation Process
Up: Galactic Scale Star Formation
Previous: Group Velocity
Contents
Kohji Tomisaka
2007-07-08


