



Next: Subcritical Cloud vs Supercritical
Up: Virial Analysis
Previous: Virial Analysis
Contents
Consider here the effect of the magnetic field.
In the magnetized medium, the Lorentz force
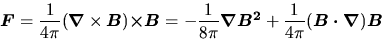 |
(4.27) |
works in the ionized medium.
The first term of equation (4.27), which is called the magnetic pressure,
has an effect to support the cloud against the self-gravity.
The virial analysis is also applicable to the magnetohydrostatic clouds.
The terms related to the magnetic fields are
where 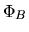 represents a magnetic flux and it is assumed to be conserved if we change the radius,
represents a magnetic flux and it is assumed to be conserved if we change the radius,
 , that is
, that is
 .
Equation (4.23) becomes
.
Equation (4.23) becomes
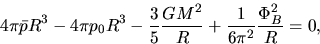 |
(4.29) |
where we ignored the term
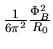 .
The last two terms are rewritten as
.
The last two terms are rewritten as
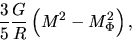 |
(4.30) |
where 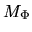 is defined as
is defined as
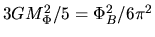 .
.
This shows the effects of the magnetic fields:
- B-fields effectively reduce the gravitational mass as
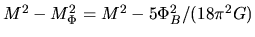 .
This plays a part to support a cloud.
.
This plays a part to support a cloud.
- However, even a cloud contracts (decreasing its radius from
 to
to  ), the ratio of the
gravitational to the magnetic terms keeps constant since these two terms are proportional to
), the ratio of the
gravitational to the magnetic terms keeps constant since these two terms are proportional to
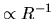 .
Thus, if the magnetic term does not work initially, the gravitational term continues to predominate over
the magnetic term.
.
Thus, if the magnetic term does not work initially, the gravitational term continues to predominate over
the magnetic term.
If 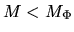 , a sum of last two terms in equation (4.29) is positive.
Since the second term of rhs of equation (4.25) is positive,
there is one
, a sum of last two terms in equation (4.29) is positive.
Since the second term of rhs of equation (4.25) is positive,
there is one 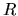 which satisfies equation (4.29) irrespective of the external pressure
which satisfies equation (4.29) irrespective of the external pressure 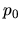 .
While, if
.
While, if 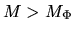 , there is a maximum allowable external pressure
, there is a maximum allowable external pressure 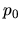 .
Therefore,
.
Therefore, 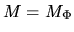 gives a criterion whether the magnetic fields work to support the cloud
or not.
More realistic calculation [Mouschovias (1976a,1976b), Tomisaka et al (1988)] gives us a criterion
gives a criterion whether the magnetic fields work to support the cloud
or not.
More realistic calculation [Mouschovias (1976a,1976b), Tomisaka et al (1988)] gives us a criterion
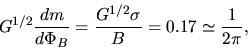 |
(4.31) |
where 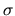 and
and 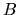 means the column density and the magnetic flux density.
A cloud with a mass
means the column density and the magnetic flux density.
A cloud with a mass
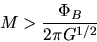 |
(4.32) |
is sometimes called magnetically supercritical, while that with
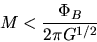 |
(4.33) |
is magnetically subcritical.
More precisely speaking, the criterion showed in equations (4.32) and
(4.33) should be applied for a cloud which has a much larger mass than the
Bonnor-Ebert mass.
That is, even without magnetic fields, the cloud less-massive than the Bonnor-Ebert mass has a hydrostatic
configuration shown in Figure 4.2 (left).
The cloud with central density of 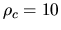 has a stable density distribution.
To fit the numerical results, Tomisaka et al (1988) obtained an expression for the critical mass
when the cloud has a mass-to-flux ratio
has a stable density distribution.
To fit the numerical results, Tomisaka et al (1988) obtained an expression for the critical mass
when the cloud has a mass-to-flux ratio 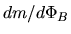 , the isothermal sound speed
, the isothermal sound speed 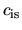 ,
and the external pressure
,
and the external pressure 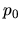 as
as
![\begin{displaymath}
M_{cr}=1.3\left\{ 1-\left[\frac{1/2\pi}{G^{1/2}d m/d \Phi_B ...
..._{r=0}}\right]^2\right\}^{-3/2}\frac{c_s^4}{p_0^{1/2}G^{3/2}}.
\end{displaymath}](img950.png) |
(4.34) |
This shows that the critical mass is a decreasing function of the mass-to-flux ratio or increasing function
of the magnetic flux.
And the critical mass becomes much larger than the Bonnor-Ebert mass
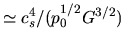 only when the mass-to-flux ratio at the center of the cloud is reaching
only when the mass-to-flux ratio at the center of the cloud is reaching 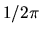 at which the term in the curry bracket goes to zero.
Hereafter, we call here the cloud/cloud core with mass larger than the critical mass
at which the term in the curry bracket goes to zero.
Hereafter, we call here the cloud/cloud core with mass larger than the critical mass 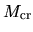 a supercritical cloud/cloud core.
The cloud/cloud core less-massive than the critical mass is subcritical.
a supercritical cloud/cloud core.
The cloud/cloud core less-massive than the critical mass is subcritical.




Next: Subcritical Cloud vs Supercritical
Up: Virial Analysis
Previous: Virial Analysis
Contents
Kohji Tomisaka
2007-07-08
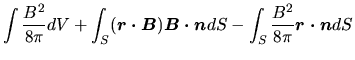
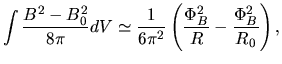
![]() has a stable density distribution.
To fit the numerical results, Tomisaka et al (1988) obtained an expression for the critical mass
when the cloud has a mass-to-flux ratio
has a stable density distribution.
To fit the numerical results, Tomisaka et al (1988) obtained an expression for the critical mass
when the cloud has a mass-to-flux ratio ![]() , the isothermal sound speed
, the isothermal sound speed ![]() ,
and the external pressure
,
and the external pressure ![]() as
as