



Next: Protostellar Evolution of Supercritical
Up: Dynamical Collapse
Previous: Dynamical Collapse
Contents
Inside-out Collapse Solution
In 1977 Shu found another self-similar solution which is realized after a central protostar with
infinitesimal mass is formed in the singular isothermal sphere solution.
The gas begins to accrete to the protostar.
Outside the region where the accretion occurs, the initial SIS is kept unchanged,
since the SIS is a hydrostatic solution.
And the front of accretion expands radially outward in time.
Since the inflow region expand outwardly, he called it the inside-out collapse solution.
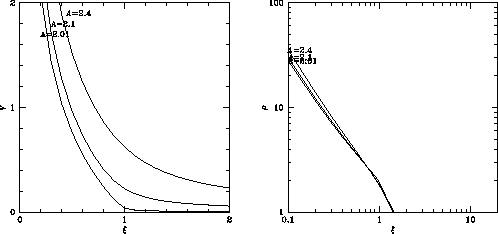
In Figure 4.7, the evolution is shown for density and inflow velocity.
This solution gives the evolution of a protostellar core formed in a subcritical cloud/cloud core.
Using equations (4.65) and (4.66) and assuming the inflow velocity should reduce at large radius,
we obtain
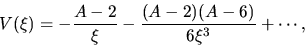 |
(4.69) |
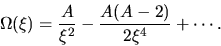 |
(4.70) |
Since
 means
means
 (if
(if 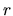 is finite),
is finite),
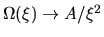 means that
means that
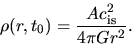 |
(4.71) |
Comparing with the SIS, when 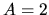 this gives the SIS and when
this gives the SIS and when 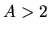 this gives a density distribution
in which the pressure is inefficient and the cloud is contracting.
The solution with
this gives a density distribution
in which the pressure is inefficient and the cloud is contracting.
The solution with 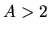 is obtained by a procedure as
(1) at a sufficiently large radius
is obtained by a procedure as
(1) at a sufficiently large radius 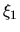 , calculate
, calculate 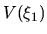 and
and 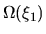 .
(2) from these values, integrate equations (4.59) and (4.60) inwardly.
Figure 4.7 show the solution of this type.
The solution with
.
(2) from these values, integrate equations (4.59) and (4.60) inwardly.
Figure 4.7 show the solution of this type.
The solution with 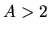 inflow speed is accelerated towards the center.
Decreasing
inflow speed is accelerated towards the center.
Decreasing 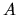 (
(
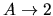 ), it is shown that an outer part
), it is shown that an outer part
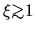 reaches
reaches
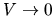 .
For
.
For 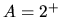 , the solution reaches the singular line
, the solution reaches the singular line 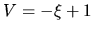 at
at 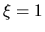 (
(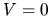 )
4.2.
Since
)
4.2.
Since 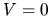 and
and 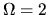 at
at 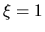 , this solution with
, this solution with 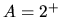 converges to the SIS at
converges to the SIS at 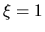 .
This means that if there is an infinitesimally small amount of excess mass at the center of SIS,
the accretion begins from the center while outside a radius the cloud is left static.
The inner part of the solution
.
This means that if there is an infinitesimally small amount of excess mass at the center of SIS,
the accretion begins from the center while outside a radius the cloud is left static.
The inner part of the solution
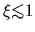 ,
, 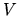 and
and 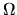 are well expressed
as
are well expressed
as
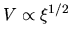 and
and
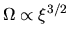 .
.
Figure 4.7:
Self-similar solution which shows the inside-out collapse. (Left:) Infall velocity (
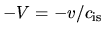 )
is plotted against the similarity variable
)
is plotted against the similarity variable
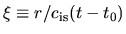 .
Three curves correspond to models
.
Three curves correspond to models 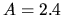 , 2.1, and 2.01.
(Right:) Density (
, 2.1, and 2.01.
(Right:) Density (
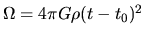 ) is plotted against the similarity variable
) is plotted against the similarity variable
 .
.
 |
The power-law distributions of
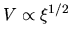 and
and
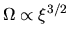 are explained as follows:
Conservation of the total energy of an inflowing gas shell is expressed as
are explained as follows:
Conservation of the total energy of an inflowing gas shell is expressed as
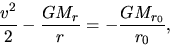 |
(4.72) |
where 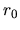 denotes the initial radius of a gas shell and
denotes the initial radius of a gas shell and 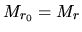 represents the
mass inside the gas shell.
Neglecting
represents the
mass inside the gas shell.
Neglecting 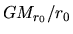 compared with the term
compared with the term 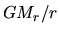 ,
this gives
,
this gives
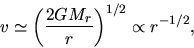 |
(4.73) |
where we assumed a major part of 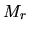 comes from the mass of a protostar
comes from the mass of a protostar 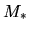 , that is,
, that is,
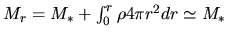 Since the average density inside the radius
Since the average density inside the radius 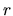
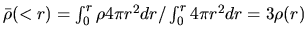 for SIS distribution,
the time necessary for a gas shell to reach the center is proportional to
for SIS distribution,
the time necessary for a gas shell to reach the center is proportional to
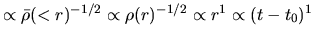 ,
where we used a fact that the front of accretion expands with a constant speed
,
where we used a fact that the front of accretion expands with a constant speed 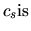 .
This means that the time necessary for the gas shell to travel from the radius of the accretion wave front
to the center is proportional to
.
This means that the time necessary for the gas shell to travel from the radius of the accretion wave front
to the center is proportional to 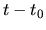 .
Since the mass of the shell which begins accretion in a unit time is equal to
.
Since the mass of the shell which begins accretion in a unit time is equal to
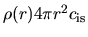 and is constant irrespective of
and is constant irrespective of 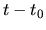 .
These two facts indicate that the mass accretion rate is constant in time.
That is,
.
These two facts indicate that the mass accretion rate is constant in time.
That is,
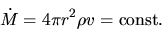 |
(4.74) |
Since the mass swept by the sound wave per unit time is equal to
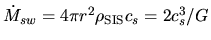 ,
the accretion rate is proportional to
,
the accretion rate is proportional to 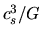 .
Shu (1977) obtained the accretion rate
.
Shu (1977) obtained the accretion rate
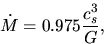 |
(4.75) |
for SIS 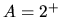 .
Using this equation, equations (4.73) and (4.74)
indicate that the spatial density
distribution is expressed by a power-law as
.
Using this equation, equations (4.73) and (4.74)
indicate that the spatial density
distribution is expressed by a power-law as
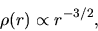 |
(4.76) |
which is valid for the region except for the vicinity of the front of the accretion.




Next: Protostellar Evolution of Supercritical
Up: Dynamical Collapse
Previous: Dynamical Collapse
Contents
Kohji Tomisaka
2007-07-08

![]() and
and
![]() are explained as follows:
Conservation of the total energy of an inflowing gas shell is expressed as
are explained as follows:
Conservation of the total energy of an inflowing gas shell is expressed as