


Next: Expression for Momentum Density
Up: Basic Equation of Fluid
Previous: Lagrangian and Euler Equations
Contents
Another basic equation comes from the mass conservation.
This is often called the continuity equation, which relates the change of the volume to its density.
Consider a fluid element whose volume is equal to 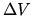 .
The mass contained in the volume is constant. Thus
.
The mass contained in the volume is constant. Thus
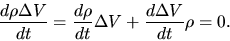 |
(A.8) |
The variation of the volume
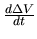 is rewritten as
is rewritten as
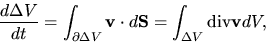 |
(A.9) |
where
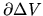 represents the surface of the fluid element
represents the surface of the fluid element  .
From equations (A.8) and (A.9),
we obtain the mass continuity equation for Lagrangian time derivative as
.
From equations (A.8) and (A.9),
we obtain the mass continuity equation for Lagrangian time derivative as
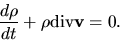 |
(A.10) |
Using equation (A.6) this is rewritten to Eulerian form as
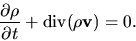 |
(A.11) |
Basic equations using the Lagrangian derivative are equations (A.3) and
(A.10), while those of the Euler derivative are equations
(A.7) and (A.11).
Subsections



Next: Expression for Momentum Density
Up: Basic Equation of Fluid
Previous: Lagrangian and Euler Equations
Contents
Kohji Tomisaka
2007-11-02
![]() .
The mass contained in the volume is constant. Thus
.
The mass contained in the volume is constant. Thus