| (4.107) |
Gas accreting onto the protostar generates energy as follows
| (4.107) |
The central temperature increases with time.
Finally thermonuclear fusion reaction of Deuterium
![]() begins.
Before Deuterium burning begins, the protostar is radiative, that is,
the energy is transported radiatively.
begins.
Before Deuterium burning begins, the protostar is radiative, that is,
the energy is transported radiatively.
When a fresh gas of ![]() accrets,
thermal energy of
accrets,
thermal energy of
![]() increases.
Virial theorem (eq.[2.120]) requires
the potential energy must decrease (increase in the absolute volume) at
increases.
Virial theorem (eq.[2.120]) requires
the potential energy must decrease (increase in the absolute volume) at
| (4.108) |
When the free-falling fresh gas accrets on the static star,
an accretion shock forms.
Since the gas temperature is increased with passing the shock front,
temperature of the postshock gas, ![]() ,
is much higher than that of the radiation,
,
is much higher than that of the radiation, ![]() .
Thus, the postshock gas cools very effectively.
The postshock region with
.
Thus, the postshock gas cools very effectively.
The postshock region with ![]() is called radiative relaxation region.
The outgoing luminosity at the accretion shock is much larger than
that inside of the radiative relaxation region.
is called radiative relaxation region.
The outgoing luminosity at the accretion shock is much larger than
that inside of the radiative relaxation region.
In the case of low mass stars
since the Kelvin-Helmholtz contraction time
![]() (
(![]() represent the luminosity at the base of the radiative relaxation region)
is much longer than the acctretion time scale
represent the luminosity at the base of the radiative relaxation region)
is much longer than the acctretion time scale
![]() .
This gives
.
This gives
![]() is much larger than
is much larger than ![]() ,
which is consistent with the above statement that
in the radiative relaxation region a large amount of accretion luminosity
is radiated away.
Since
,
which is consistent with the above statement that
in the radiative relaxation region a large amount of accretion luminosity
is radiated away.
Since
![]() , the specific entropy inside the relaxation region
is essentially frozen to that when the gas obtained passing through
the relaxtaion region.
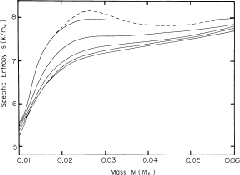
Figure 4.19 taken from Stahler, Shu & Taam (1982) shows the distribution of the specific entropy against the accumulated mass
, the specific entropy inside the relaxation region
is essentially frozen to that when the gas obtained passing through
the relaxtaion region.
Figure 4.19 taken from Stahler, Shu & Taam (1982) shows the distribution of the specific entropy against the accumulated mass ![]() .
The bottom curve corresponds to the state before the nuclear burning begins
when no entropy generation occurs.
The temperature increases with mass,
bacause the star must be compressed to support an extra mass.
After the temperature becomes high enough for Deuterium burning reaction
.
The bottom curve corresponds to the state before the nuclear burning begins
when no entropy generation occurs.
The temperature increases with mass,
bacause the star must be compressed to support an extra mass.
After the temperature becomes high enough for Deuterium burning reaction
![]() as
as
![]() ,
an extra energy is liberated by the nuclear fusion reaction.
This increases the specific entropy mainly in the offcenter region.
Figure 4.19 clearly shows that shell Deuterium burning
occurs at
,
an extra energy is liberated by the nuclear fusion reaction.
This increases the specific entropy mainly in the offcenter region.
Figure 4.19 clearly shows that shell Deuterium burning
occurs at
![]() .
.
 |