前節の式(1.19)、(1.20)、(1.21)では、 流束の空間微分に関する部分をどうとるかということには触れなかった。 流体力学の数値解法は、つまるところ、 空間微分に関する差分と時間微分に関する差分をどのようにとるか、 ということに集約できる。
式(1.12)を
このような差分に書き直した時、
グリッドの中心での値である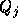
に対して、
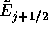や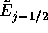
はグリッドの境界での値で
あるべきである。
このときどのようにして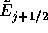
などの量を決めれば良いのだろうか。
ここで、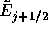
を
、
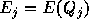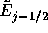を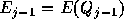
とすれば、
空間後退差分・時間前進差分のスキームが
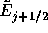を
、
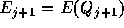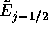を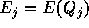
とすれば、
空間前進差分・時間前進差分のスキームができる。
空間中心差分のスキームには、
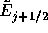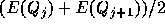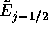を
、
を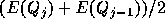
のように
すれば良いことは容易にわかるだろう。
数値流体力学の計算方法とは、この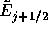
などの流束の値を、
どのよう決めればよいかという問題に帰着する。
このような立場に立ってスキームに現れる
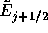などの流束
のことを数値流束と呼ぶ。
数値流速の決め方こそ数値流体力学の計算方法のポイントといえる。
数値計算スキームによってこの数値流束のとりかたは異なるが、いくつかの
例について後に見ることになる。
