空間１次精度のスキーム

とすれば、時間については１次精度前進差分、 空間については１次精度後退差分をとったスキームができる。 プログラムは

for j:=0 to jm do
  w[j]:=u[j];
for j:=1 to jm do
  u[j]:=w[j]-nu*(w[j]-w[j-1]);

  
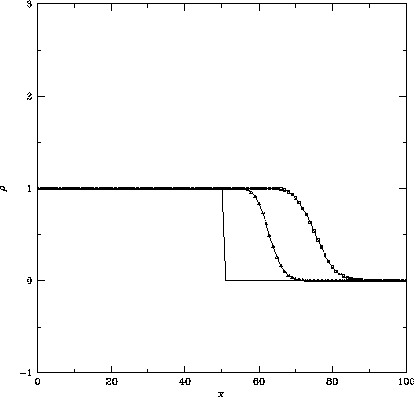
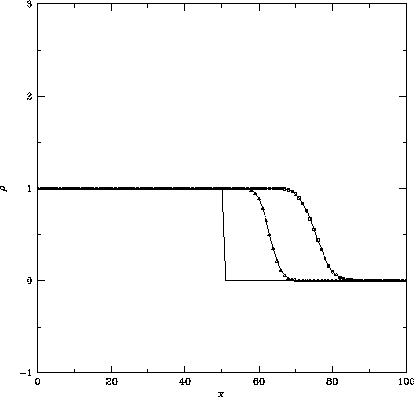
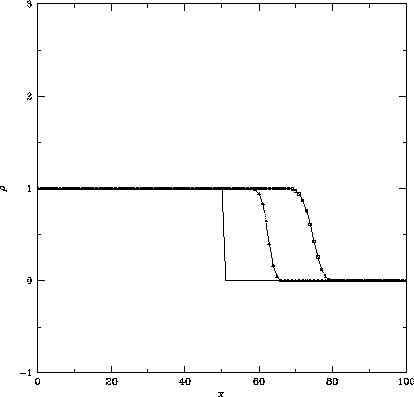
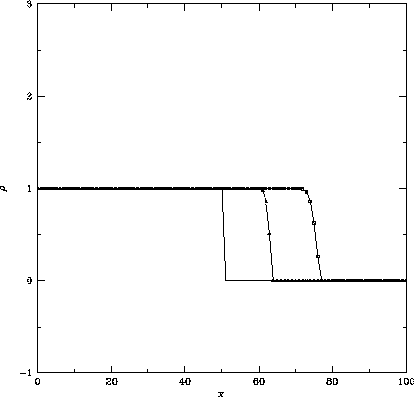
Figure 1.5: 図1.2とおなじ。ただし採用した計算スキームは 空間１次精度後退差分をとったスキームで、 クーラン数は左から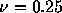、、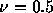、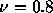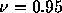をとっている。

この問題では、現象は左から右へ伝わってゆくので、それをとらえられるように、 空間については後退差分をとった。 図1.5から、空間１次精度のスキームは、密度の飛びの部分で余分な振動を起 こさないことがわかる。 しかし同時に、密度の飛びの部分が時間が進むにつれて、ぼやけてゆくこと もわかる。 このように、空間１次精度のスキームは余分な振動を起こさない良い性質を もっているが、飛びの部分がぼやけてゆくという悪い性質を持っていることが わかる。 テイラー展開を用いてこのスキームにどの程度の誤差が含まれているかを 見てみると、式(1.38)は元の微分方程式(1.24)に ２つ余分な項を含んでおり

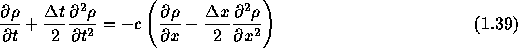
と等しくなることがわかる。 ここで、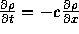に気をつけて変形すると、これは

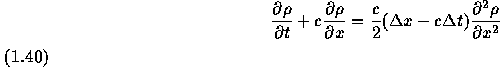
となる。この式で

のようにとると、右辺は正の拡散係数を持つ 拡散項であることがわかる。 つまりこのようにして作った空間１次精度のスキームは正の拡散係数を持つ 拡散項を差分化にともなう誤差として含むために余分の振動を生じなくなって いることがわかる。

ここで式(1.41)は早さcで伝わる現象について 時間進化を計算する場合に、情報が格子１つ分以上伝搬する時間以上に 時間ステップをとってはならないという条件に相当しており、 数値流体力学で非定常問題を解く場合の時間ステップに関する条件を 与えるものである。 これは、Courant, Friedrich, Lewy(1928)条件（CFL条件）と呼ばれる。