
前節で見たように、空間2次精度のスキームでは、余分な振動が発生した。 空間1次精度のスキームは余分な振動は発生しなかったが、密度の飛びは 時間がすすむとともに鈍ってゆくことがわかった。 これらの差はどこからくるのだろうか。 差分方程式に含まれる元の微分方程式からのずれ(誤差)に 起因することは前に述べた。
ここでは、von Neumannの安定性解析を使って余分な振動や解の鈍りと差分スキーム の間の関係を定量的に見てゆく。 解をフーリエ分解して、

と書く。ここでjは格子点の番号で、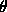 は格子間隔
は格子間隔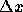 を単位とした
波数つまり
を単位とした
波数つまり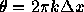 で
で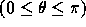 。
。
この式をスキームに代入し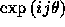 に比例する項を取り出す。
FTCSスキーム
に比例する項を取り出す。
FTCSスキーム

に対しては、
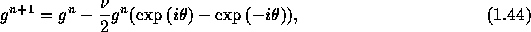
となる。これから複素振幅gが
となっていることがわかる。
この問題では厳密解は、
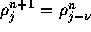 を満足していなければならないので、
を満足していなければならないので、
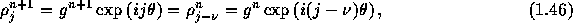
が成り立たねばならず、 これから厳密解に対する複素振幅gは

で与えられる。
これは当然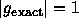 で、厳密解では位相だけが動いてゆくことになる。
これからどれだけ異なっているかを調べれば、差分化にともなって、微分方程式の厳密
解からずれた部分がわかることになる。
で、厳密解では位相だけが動いてゆくことになる。
これからどれだけ異なっているかを調べれば、差分化にともなって、微分方程式の厳密
解からずれた部分がわかることになる。
複素振幅gの絶対値はある波の1ステップ後との振幅の比を与えるが、 式(1.45)に対しては

で与えられる。
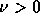 に対しては波数
に対しては波数 の波は増幅されることがわかる。
の波は増幅されることがわかる。
つぎに複素振幅gの位相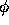 は、
は、

で、厳密解の位相に対する比は
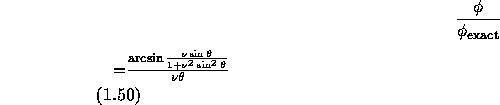
のように計算できる。これを図に書くと図1.6のようになる。
|g|と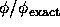 を図示するMathematicaのプログラムは
を図示するMathematicaのプログラムは
G[nu_,theta_]=Sqrt[1+nu^2 Sin[theta]^2]
Plot[G[0.5,theta],{theta,0,Pi},Frame -> True]
および
Phi[nu_,theta_]=ArcSin[nu Sin[theta]/Sqrt[1+nu^2 Sin[theta]^2]]/(nu theta)
Plot[Phi[0.5,theta],{theta,0.0001,Pi},Frame->True]
である。
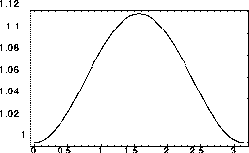
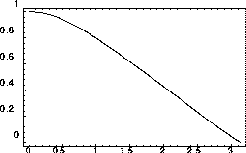
Figure 1.6: FTCSスキームで、
クーラン数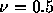 でにする複素振幅gの絶対値(左)と
複素振幅gの位相
でにする複素振幅gの絶対値(左)と
複素振幅gの位相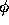 の厳密解の位相に対する比(右)。
の厳密解の位相に対する比(右)。
ここで、複素振幅gの絶対値が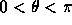 (0と
(0と 以外)に対して
1を越えているので、初期値に含む周期的な波はかならず増幅される
ことになることがわかる。
また、
以外)に対して
1を越えているので、初期値に含む周期的な波はかならず増幅される
ことになることがわかる。
また、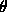 の大きな(短波長の)波の方で厳密解に比べて、
位相が遅れることもわかる。図1.2で短波長の波が後方に
取り残されているように見えることもこのように説明される。
の大きな(短波長の)波の方で厳密解に比べて、
位相が遅れることもわかる。図1.2で短波長の波が後方に
取り残されているように見えることもこのように説明される。
同じようにして、Laxのスキームでは、

となり、絶対値と位相の比は、

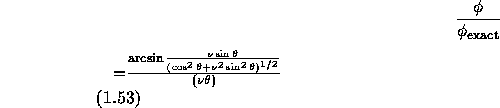
で与えられる。 これを図示するMathematicaのプログラムは
G[nu_,theta_]=Sqrt[Cos[theta]^2+nu^2 Sin[theta]^2]
Plot[G[0.5,theta],{theta,0,Pi},Frame -> True]
Phi[nu_,theta_]=ArcCos[Cos[theta]/G[nu,theta]]/(nu theta)
Plot[Phi[0.5,theta],{theta,0.0001,Pi},Frame->True]
のようになる。
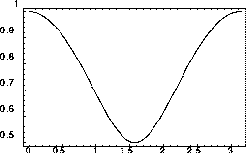
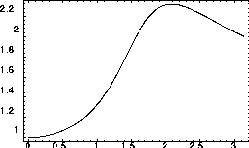
Figure 1.7: Laxスキームで、
クーラン数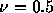 に対する複素振幅gの絶対値(左)と
複素振幅gの位相
に対する複素振幅gの絶対値(左)と
複素振幅gの位相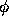 の厳密解の位相に対する比(右)。
の厳密解の位相に対する比(右)。
図1.7(左)を見ると、すべての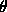 で|g|<1であり、
周期的な振動はその振幅が減少してゆくことがわかる。
特に、
で|g|<1であり、
周期的な振動はその振幅が減少してゆくことがわかる。
特に、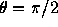 つまり4グリッドで1波長となる波が大きく減衰することが
わかる。
図1.7(右)からは、
つまり4グリッドで1波長となる波が大きく減衰することが
わかる。
図1.7(右)からは、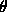 の大きい波に対して、
正の位相誤差とを生じており、Laxスキームで飛びが鈍ってゆくにつれて
前方に崩れてゆく構造がこれが原因となっていると見ることができる。
の大きい波に対して、
正の位相誤差とを生じており、Laxスキームで飛びが鈍ってゆくにつれて
前方に崩れてゆく構造がこれが原因となっていると見ることができる。
また、1次のスキームに対しても同様の解析は可能で、

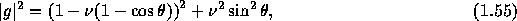

で、図1.8で複素振幅gの絶対値は、大きい波数に対して
減少しており、短波長の波ほど減衰しやすいことがわかる。
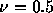 の場合は
の場合は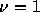 の場合とともに複素振幅gの位相誤差は0になるが
(図1.8右)、
の場合とともに複素振幅gの位相誤差は0になるが
(図1.8右)、
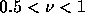 では
では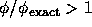 で前進位相誤差を、
で前進位相誤差を、
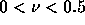 では
では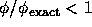 で遅延位相誤差を持つ。
で遅延位相誤差を持つ。
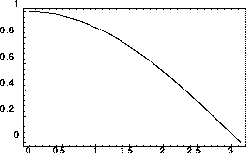
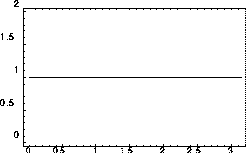
Figure: 図1.6と同じ、ただし、1次精度空間後退差分スキームで、
クーラン数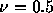 でにする複素振幅gの絶対値(左)と
複素振幅gの位相
でにする複素振幅gの絶対値(左)と
複素振幅gの位相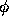 の厳密解の位相に対する比(右)。
の厳密解の位相に対する比(右)。