１次元の流体の基礎方程式は、３つの式をベクトルのように並べて書いて、
と書ける ただし、QとEは物理量をならべたベクトルで、
である。ここで、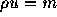
と書いて従属変数を
に書き直すと、Eの方はこれを使って
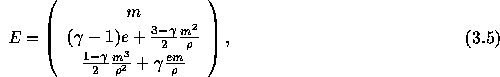
のように書ける。
式(3.2))を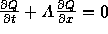
のように書き直す
ことを考える
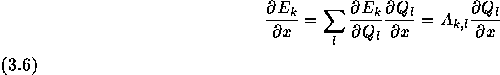
のように書きなおせて、ここに出てくる
を流束ヤコビアンと呼ぶ。 具体的に書き下すと、
保存量Q（質量密度、運動量密度、エネルギー密度）を使って
書いた式の代わりに、基本量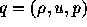
（密度、速度、圧力）を用いて
非保存形の式を書くこともできて、
のように書くこともできる。シンボリックな書き方をすれば
となる。Mは基本量qに関する流束ヤコビアンである。
