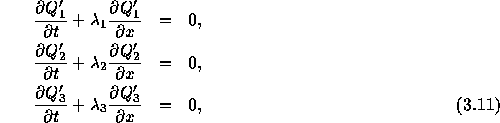
式(3.3)や(3.9)を第１章で見たadvectionの形に書き直すこと を考える。 すなわち、
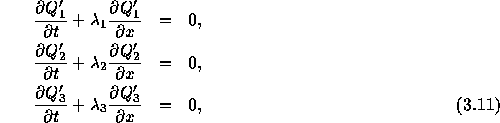
の形に変形するのである。 これができれば、それぞれの式に第２章でみた 高精度風上差分の方法を適応することによって 流体力学の方程式も解くことができる。
式(3.9)を上の形に書き直すのは行列Mを対角化するという ことに相当する。 行列Mを対角化するとは、
となる固有ベクトル xと固有値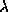
をもとめることに帰着する。
これは、
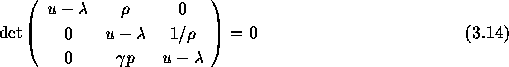
の特性方程式の解を求めると、
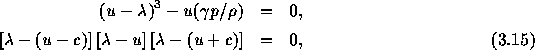
であるから、固有値は音速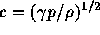
を使って、
であることがわかる。
d={{u,rho,0},{0,u,1/rho},{0,g p,u}}
Simplify[Eigenvalues[d]]/.Sqrt[g]Sqrt[p]/Sqrt[rho]-> cs
{u, -cs + u, cs + u}
この速度は、それぞれ、物体の流れる速度(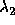
)、物体に対して
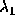左方向に伝わる音波の速度(
)、おなじく右方向に伝わる音波
の速度(
)である。
さらに、固有ベクトルは
を解いて、
から
となる。 同じようにして、
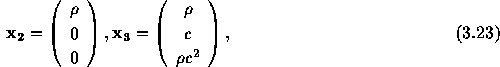
となることがわかる。この固有ベクトルを横に並べた行列（右固有行列）
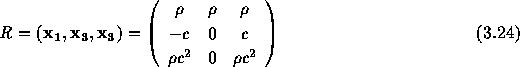
を考えると、
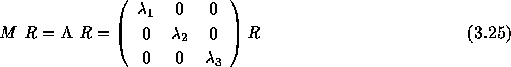
となる。
このR行列の逆行列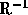
をこの式の左から掛けると、
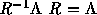ゆえ、
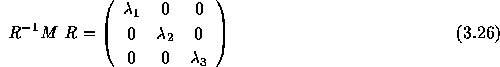
となる。
Rの逆行列は
R={{rho,rho,rho},{-c,0,c},{rho c^2,0,rho c^2}}
2 2
{{rho, rho, rho}, {-c, 0, c}, {c rho, 0, c rho}}
Inverse[R]//MatrixForm//TeXForm
のようにして求められる。
式(3.10)に左から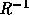
を掛けると、
となるが、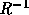
が空間、時間の微小部分ついては一定と考えられるならば、
であり、３つの独立したスカラー方程式に分離できたことになる。
それぞれは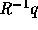
の３つの成分それぞれに対するadvectionの方程式
に合致している。
ただし、その速度が
、
、
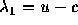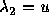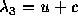と
異なっていることが違っている。
それぞれの変数に対して風上差分を考えることは第２章と同じようにできる。
これが流体力学に関する高解像度風上差分の基本である。
なお流束ヤコビアンAから保存量に対する固有行列を求めておくと
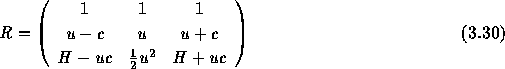
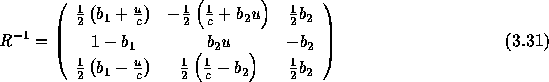
である。ただしここで
を表す。