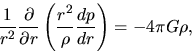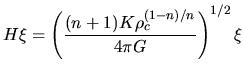Next: Magnetohydrostatic Configuration
Up: Hydrostatic Equilibrium
Previous: Hydrostatic Equilibrium
Contents
Polytrope
Figure C.1:
Solutions of eq.(C.6) are plotted for indices of
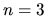 or
or 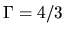 (the most extended one),
(the most extended one), 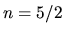 or
or 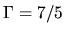 (the middle), and
(the middle), and
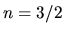 or
or 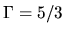 (the most compact one).
For
(the most compact one).
For 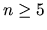 gas extends infinitely and the solution has no zero-point.
gas extends infinitely and the solution has no zero-point.
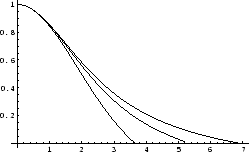 |
If we choose the polytropic equation of stateC.1,
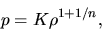 |
(C.1) |
the hydrostatic balance is expressed by
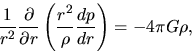 |
(C.2) |
where we used equations (4.1) and
(4.2).
A hydrostatic gaeous star composed with a polytropic gas is called polytrope.
Normalizing the density, pressure and radius as
we obtain a normalized equation as
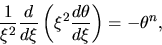 |
(C.6) |
which is called Lane-Emden equation of index 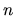 .
The boundary condition at the center of polytrope should be
.
The boundary condition at the center of polytrope should be
at 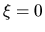 .
Solution of this equation is plotted for several
.
Solution of this equation is plotted for several 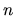 in Figure C.1.
in Figure C.1.
Mass of the polytrope is written down as
where 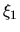 represents the zero point of
represents the zero point of 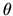 or the
surface radius normalized by
or the
surface radius normalized by 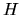 .
For
.
For 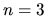 or
or
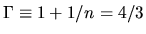 ,
equation (C.9) reduces to
,
equation (C.9) reduces to
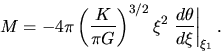 |
(C.10) |
Thus, the mass does not depend on the central density for 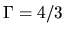 polytrope.
For
polytrope.
For 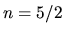 or
or
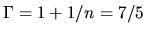 ,
, 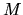 is written down as
is written down as
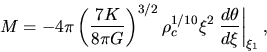 |
(C.11) |
where 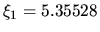 and
and
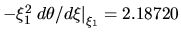 .
Polytrope with
.
Polytrope with 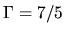 gas, the mass-density relation
becomes
gas, the mass-density relation
becomes
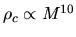 .
While, for
.
While, for 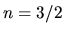 of
of
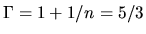 ,
, 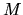 is written down as
is written down as
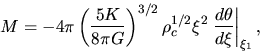 |
(C.12) |
where 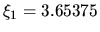 and
and
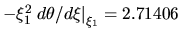 .
.




Next: Magnetohydrostatic Configuration
Up: Hydrostatic Equilibrium
Previous: Hydrostatic Equilibrium
Contents
Kohji Tomisaka
2007-07-08