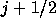 の物理量を評価するRoe平均にとられる
の物理量を評価するRoe平均にとられる
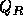 と
と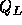 をMUSCLで内挿されたグリッド境界の値をとる(式(2.31)、
(2.32))。
をMUSCLで内挿されたグリッド境界の値をとる(式(2.31)、
(2.32))。
FDS法にMUSCL法を適用するには、次のようにすればよい。
(1)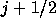 の物理量を評価するRoe平均にとられる
の物理量を評価するRoe平均にとられる
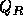 と
と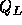 をMUSCLで内挿されたグリッド境界の値をとる(式(2.31)、
(2.32))。
をMUSCLで内挿されたグリッド境界の値をとる(式(2.31)、
(2.32))。
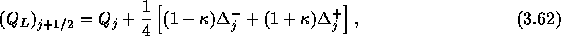
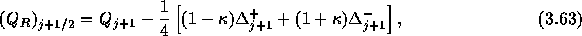
ここで、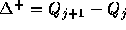 であり、
であり、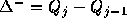 である。
である。
このとき、制限関数を導入し解の単調性を維持するのは2.3節と同様である。
ただし、MUSCL内挿をどの物理量に対して行なうかは任意性がある。
経験的には、基本量(密度、速度、圧力)を内挿して、それから他の量を
求める方がうまく行くといわれている。
(2)次に数値流束を
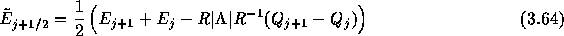
から
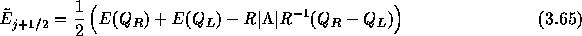
に高精度化する。この部分は次のようにプログラムに書けて、
E1[j]:=0.5*(mR[j]+mL[j]
-w[1,1]*(rhoR[j]-rhoL[j])
-w[1,2]*(mR[j]-mL[j])
-w[1,3]*(eR[j]-eL[j]));
E2[j]:=0.5*(gam1*(eR[j]+eL[j])+gam3/2*(Sqr(mR[j])/rhoR[j]+Sqr(mL[j])/rhoL[j])
-w[2,1]*(rhoR[j]-rhoL[j])
-w[2,2]*(mR[j]-mL[j])
-w[2,3]*(eR[j]-eL[j]));
E3[j]:=0.5*(gamma*(eR[j]*mR[j]/rhoR[j]+eL[j]*mL[j]/rhoL[j])
-gam1/2*(Sqr(mR[j]/rhoR[j])*mR[j]+Sqr(mL[j]/rhoL[j])*mL[j])
-w[3,1]*(rhoR[j]-rhoL[j])
-w[3,2]*(mR[j]-mL[j])
-w[3,3]*(eR[j]-eL[j]));
となる。図3.8にこの方法で求めたテスト問題の解を掲げる。
衝撃波面の後ろ側の振動もほとんど押えられ、
接触不連続面や衝撃波面が時間的に鈍ってゆくことも空間1次精度の
図3.6に比べて改善されていることがわかる。
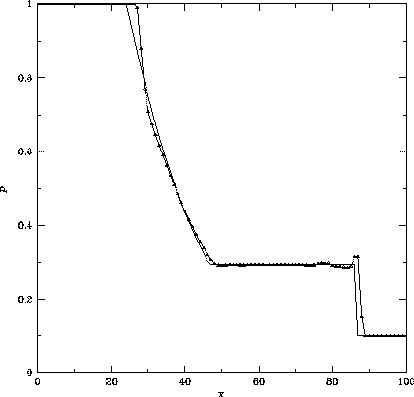
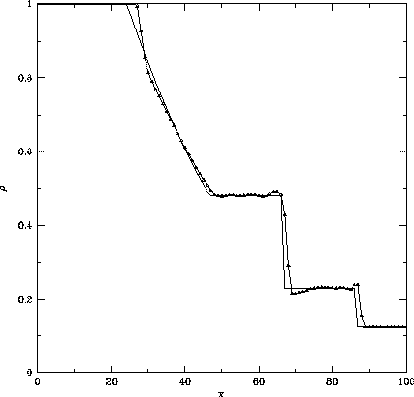
Figure 3.8: MUSCLで2次精度化したFlux Difference Splitting法
による衝撃波管問題の解。
初期条件は同じ。